题目内容
定义函数f（x）=-x3+ax2+b（a，b∈R）．
（Ⅰ）f′（x）是f（x）的导函数，若不等式|f′（x）|≤1对任意的x∈[0，1]恒成立，求实数a的取值范围；
（Ⅱ）若b＜0，函数f（x）有两个零点满足x1∈（0，1），x2∈（1，2），求a-2b的取值范围．
（Ⅰ）f′（x）是f（x）的导函数，若不等式|f′（x）|≤1对任意的x∈[0，1]恒成立，求实数a的取值范围；
（Ⅱ）若b＜0，函数f（x）有两个零点满足x1∈（0，1），x2∈（1，2），求a-2b的取值范围．
考点：简单线性规划,利用导数研究函数的单调性
专题：导数的概念及应用
分析：（Ⅰ）求出函数的导数根据不等式|f′（x）|≤1对任意的x∈[0，1]恒成立，结合一元二次函数的性质即可求实数a的取值范围；
（Ⅱ）根据函数零点的取值范围，建立不等式关系，利用线性规划的知识即可得到结论．
（Ⅱ）根据函数零点的取值范围，建立不等式关系，利用线性规划的知识即可得到结论．
解答：
（Ⅰ）∵f（x）=-x3+ax2+b（a，b∈R）．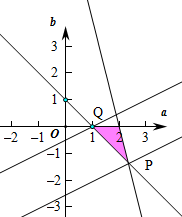
∴f′（x）=）=-3x2+2ax，
当a≤0，必须有|f′（1）|≤1，解得1≤a≤2，此时不成立．
当0＜
＜1，必须|f′（1）|≤1且|f′（
）|≤1，解得1≤a≤
，
当a≥3，必须|f′（1）|≤1，解得1≤a≤2，不成立．
综上1≤a≤
．
（Ⅱ）∵f（0）=b＜0，函数f（x）有两个零点满足x1∈（0，1），x2∈（1，2），
∴
，即
，
作出可行域如图：则Q（1，0），
由
，解得
，即P（
，-
），
∴t1=a-2b=1，t2=a-2b=
+
=5，
即1＜a-2b＜5．
∴f′（x）=）=-3x2+2ax，
当a≤0，必须有|f′（1）|≤1，解得1≤a≤2，此时不成立．
当0＜
| a |
| 3 |
| a |
| 3 |
| 3 |
当a≥3，必须|f′（1）|≤1，解得1≤a≤2，不成立．
综上1≤a≤
| 3 |
（Ⅱ）∵f（0）=b＜0，函数f（x）有两个零点满足x1∈（0，1），x2∈（1，2），
∴
|
|
作出可行域如图：则Q（1，0），
由
|
|
| 7 |
| 3 |
| 4 |
| 3 |
∴t1=a-2b=1，t2=a-2b=
| 7 |
| 3 |
| 8 |
| 3 |
即1＜a-2b＜5．
点评：本题主要考查导数的应用，利用一元二次函数和线性规划的知识是解决本题的关键．综合性较强，有一定的难度．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目