题目内容
(本小题满分14分)如图,在四棱锥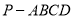 中,底面
中,底面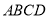 是正方形,
是正方形,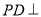 平面
平面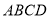 .点
.点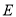 是线段
是线段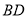 的中点,点
的中点,点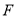 是线段
是线段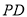 上的动点.
上的动点.

(Ⅰ)若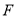 是
是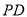 的中点,求证:
的中点,求证: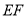 //平面
//平面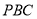 ;
;
(Ⅱ)求证: 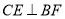 ;
;
(Ⅲ)若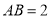 ,
,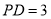 ,当三棱锥
,当三棱锥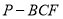 的体积等于
的体积等于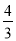 时,试判断点
时,试判断点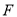 在边
在边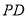 上的位置,并说明理由.
上的位置,并说明理由.
点F为边PD上靠近D点的三等分点
【解析】
试题分析:(Ⅰ)证明:
在 中,因为点E是BD中点,点F是PD中点,
中,因为点E是BD中点,点F是PD中点,
所以 //
// .
.
又因为 平面
平面 ,
, 平面
平面 ,
,
所以 //平面
//平面 .
.
(Ⅱ)证明:
因为 平面
平面 ,
,
且 平面
平面 ,
,
所以 .
.
又因为底面 是正方形,且点E是BD的中点,
是正方形,且点E是BD的中点,
所以
 .
.
因为 ,所以
,所以 平面
平面 ,
,
而 平面
平面 ,所以
,所以 .
.
(Ⅲ)点F为边PD上靠近D点的三等分点.
说明如下:
由(Ⅱ)可知, 平面
平面 .
.
又因为 平面
平面 ,
, 平面
平面 ,所以
,所以 .
.
设 . 由AB=2得
. 由AB=2得 ,
,
所以 .
.
由已知 , 所以x=2.
, 所以x=2.
因为 ,点F为边PD上靠近D点的三等分点.
,点F为边PD上靠近D点的三等分点.
考点:本题考查线线垂直的证明,等体积法求三棱锥的体积

练习册系列答案
相关题目
 ;条件q:直线y= kx+2与圆x2+y2=1相切,则p是q的( )
;条件q:直线y= kx+2与圆x2+y2=1相切,则p是q的( )
 B.
B.
 D.
D.
 ,
, ,则
,则 .
. 是两个非零的平面向量,则 “
是两个非零的平面向量,则 “ ”是“
”是“ ”的
”的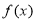 ,若存在区间
,若存在区间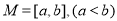 ,使得
,使得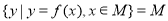 ,则称区间
,则称区间 为函数
为函数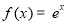 (B)
(B)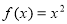 (C)
(C)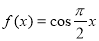 (D)
(D)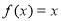
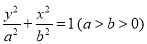 的离心率为
的离心率为 ,其四个顶点组成的菱形的面积是
,其四个顶点组成的菱形的面积是 ,O为坐标原点,若点A在直线
,O为坐标原点,若点A在直线 上,点B在椭圆C上,且
上,点B在椭圆C上,且 .
. 与圆
与圆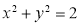 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.