题目内容
(本小题满分13分)已知椭圆C: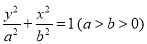 的离心率为
的离心率为 ,其四个顶点组成的菱形的面积是
,其四个顶点组成的菱形的面积是 ,O为坐标原点,若点A在直线
,O为坐标原点,若点A在直线 上,点B在椭圆C上,且
上,点B在椭圆C上,且 .
.
(1)求椭圆C的方程;
(2)求线段AB长度的最小值;
(3)试判断直线 与圆
与圆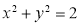 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(1)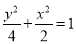 ; (2)线段AB长度的最小值为
; (2)线段AB长度的最小值为 ;(3)直线AB与圆
;(3)直线AB与圆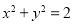 相切.
相切.
【解析】
试题分析:(1)由题设可列方程组 ,解得
,解得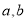 的值,从而确定椭圆C的方程;
的值,从而确定椭圆C的方程;
(2)设点A,B的坐标分别为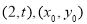 ,其中
,其中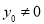 ,结合条件
,结合条件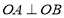 ,把
,把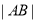 表示成
表示成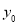 的函数再求其最值.
的函数再求其最值.
(3)设点A,B的坐标分别为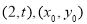 ,其中
,其中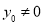 .写出直线AB的方程,求出原点到直线AB的距离
.写出直线AB的方程,求出原点到直线AB的距离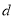 ,并结合条件
,并结合条件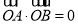 判断
判断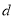 与圆的半径的关系,从而得到直线与圆的位置关系.
与圆的半径的关系,从而得到直线与圆的位置关系.
试题解析:【解析】
(1)由题意 ,解得
,解得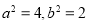 .
.
故椭圆C的标准方程为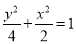 . 3分
. 3分
(2)设点A,B的坐标分别为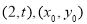 ,其中
,其中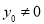 ,
,
因为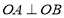 ,所以
,所以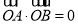 ,即
,即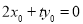 , 4分
, 4分
解得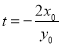 ,又
,又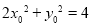 ,
,
所以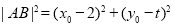
=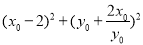
=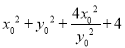
=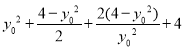 =
=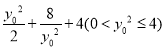 , 5分
, 5分
因为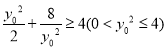 ,当且仅当
,当且仅当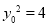 时等号成立,所以
时等号成立,所以 ,
,
故线段AB长度的最小值为 . 7分
. 7分
(3)直线AB与圆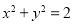 相切. 8分
相切. 8分
证明如下:
设点A,B的坐标分别为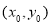 ,
,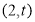 ,其中
,其中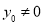 .
.
因为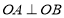 ,所以
,所以 ,即
,即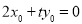 ,解得
,解得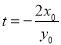 . 9分
. 9分
直线AB的方程为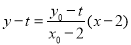 ,
,
即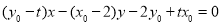 , 10分
, 10分
圆心O到直线AB的距离 , 11分
, 11分
由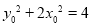 ,
,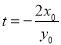 ,
,
故 
 ,
,
所以 直线AB与圆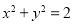 相切. 13分
相切. 13分
考点:1、椭圆的标准方程与简单几何性质;2、两点间的距离公式与点到直线的距离公式;3、直线与圆的位置关系.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 中,底面
中,底面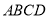 是正方形,
是正方形,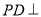 平面
平面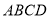 .点
.点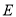 是线段
是线段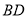 的中点,点
的中点,点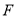 是线段
是线段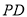 上的动点.
上的动点.
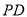 的中点,求证:
的中点,求证: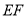 //平面
//平面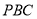 ;
;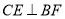 ;
; 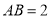 ,
,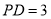 ,当三棱锥
,当三棱锥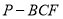 的体积等于
的体积等于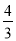 时,试判断点
时,试判断点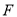 在边
在边 上的位置,并说明理由.
上的位置,并说明理由. 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,则
的图象,则 .
.
 的图形的一条对称轴经过点( ) .
的图形的一条对称轴经过点( ) .



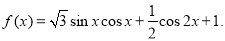
 的最小正周期;
的最小正周期; 时,求函数
时,求函数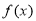 的最大值及取得最大值时的
的最大值及取得最大值时的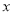 值.
值. 满足
满足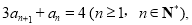 且
且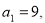 其前
其前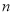 项之和为
项之和为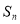 ,则满足不等式
,则满足不等式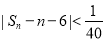 成立的
成立的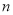 的最小值是
的最小值是 ,
, 满足约束条件
满足约束条件 则
则 的最大值是 .
的最大值是 . .
.