题目内容
【题目】已知圆![]() :
: ![]() 与定点
与定点![]() ,
, ![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设曲线![]() 与
与![]() 轴正半轴交点为
轴正半轴交点为![]() ,不经过点
,不经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于不同两点
相交于不同两点![]() ,
, ![]() ,若
,若![]() .证明:直线
.证明:直线![]() 过定点.
过定点.
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)利用椭圆定义求轨迹方程;(2)如果![]() 与
与![]() 轴不垂直,可设
轴不垂直,可设![]() ,将
,将![]() 代入
代入![]() 得
得![]() 由题设可知
由题设可知![]() 设
设![]() 则
则![]()
利用![]() ,得到
,得到![]() ,从而明确直线
,从而明确直线![]() 过定点.
过定点.
试题解析:
(Ⅰ)由已知![]() ,则
,则![]() ,
,
则点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点的椭圆,可设
为焦点的椭圆,可设![]() 的方程为:
的方程为: ![]() ,
,
由已知可得![]() ,则点
,则点![]() 的轨迹
的轨迹![]() 的方程为:
的方程为: ![]() .
.
(Ⅱ)①如果![]() 与
与![]() 轴垂直,设
轴垂直,设![]() ,由题知
,由题知![]() ,可得
,可得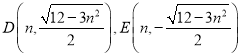 ,又
,又![]() ,
,
则![]() 得
得![]() 或
或![]() 舍去,则
舍去,则![]()
②如果![]() 与
与![]() 轴不垂直,可设
轴不垂直,可设![]() ,将
,将![]() 代入
代入![]() 得
得![]() 由题设可知
由题设可知![]()
设![]() 则
则![]()
又![]() ,
,
由![]() ,
,
故![]() ,
,
得![]()
即![]() ,则
,则![]()
解得![]() 或
或![]() (舍去)
(舍去)
![]() 时,满足
时,满足![]() ,于是
,于是![]() 即
即![]() ,恒过定点
,恒过定点![]()
又![]() ,也过点
,也过点![]()
综上可知,直线![]() 恒过定点
恒过定点![]() ,故得证.
,故得证.

 名校课堂系列答案
名校课堂系列答案【题目】某地有一企业2007年建厂并开始投资生产,年份代号为7,2008年年份代号为8,依次类推.经连续统计9年的收入情况如下表(经数据分析可用线性回归模型拟合![]() 与
与![]() 的关系):
的关系):
年份代号( | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
当年收入( | 13 | 14 | 18 | 20 | 21 | 22 | 24 | 28 | 29 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)试预测2020年该企业的收入.
(参考公式: 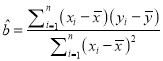
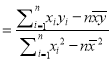 ,
, ![]() )
)
【题目】某校想了解高二数学成绩在学业水平考试中的情况,从中随机抽出![]() 人的数学成绩作为样本并进行统计,频率分布表如下表所示.
人的数学成绩作为样本并进行统计,频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
|
|
|
第2组 |
|
|
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|
合计 |
|
| |
(1)据此估计这次参加数学考试的高二学生的数学平均成绩;
(2)从这五组中抽取![]() 人进行座谈,若抽取的这
人进行座谈,若抽取的这![]() 人中,恰好有
人中,恰好有![]() 人成绩为
人成绩为![]() 分,
分,![]() 人成绩为
人成绩为![]() 分,
分,![]() 人成绩为
人成绩为![]() 分,
分,![]() 人成绩为
人成绩为![]() 分,求这
分,求这![]() 人数学成绩的方差;
人数学成绩的方差;
(3)从![]() 人的样本中,随机抽取测试成绩在
人的样本中,随机抽取测试成绩在![]() 内的两名学生,设其测试成绩分别为
内的两名学生,设其测试成绩分别为![]() ,
,![]() .
.
(i)求事件“![]() ”的概率;
”的概率;
(ii)求事件“![]() ”的概率.
”的概率.