题目内容
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() 是
是![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上.
上.
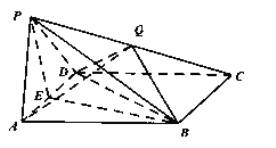
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(3)若![]() ,试求
,试求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)由线面垂直判定定理,要证线面垂直,需证![]() 垂直平面
垂直平面![]() 内两条相交直线,由
内两条相交直线,由![]() ,
,![]() 是
是![]() 的中点,易得
的中点,易得![]() 垂直于
垂直于![]() ,再由底面
,再由底面![]() 是菱形,
是菱形,![]() 得三角形
得三角形![]() 为正三角形,所以
为正三角形,所以![]() 垂直于
垂直于![]() ,(2)由线面平行判定定理,要证线面平行,需证
,(2)由线面平行判定定理,要证线面平行,需证![]() 平行于平面
平行于平面![]() 内一条直线,根据
内一条直线,根据![]() 是
是![]() 的中点,联想到取AC中点O所以OQ为△PAC中位线.所以OQ // PA注意在写定理条件时,不能省,要全面.例如,线面垂直判定定理中有五个条件,线线垂直两个,相交一个,线在面内两个;线面平行判定定理中有三个条件,平行一个,线在面内一个,线在面外一个,(3)研究体积问题关键在于确定高,由于两个底面共面,所以求
的中点,联想到取AC中点O所以OQ为△PAC中位线.所以OQ // PA注意在写定理条件时,不能省,要全面.例如,线面垂直判定定理中有五个条件,线线垂直两个,相交一个,线在面内两个;线面平行判定定理中有三个条件,平行一个,线在面内一个,线在面外一个,(3)研究体积问题关键在于确定高,由于两个底面共面,所以求![]() 的值就转化为求对应高的长度比.
的值就转化为求对应高的长度比.
试题解析:(1)因为E是AD的中点,PA=PD,所以AD⊥PE.
因为底面ABCD是菱形,∠BAD=![]() ,所以AB=BD,又因为E是AD的中点,所以 AD⊥BE.
,所以AB=BD,又因为E是AD的中点,所以 AD⊥BE.
因为PE∩BE=E,所以AD⊥平面PBE. 4分
(2)连接AC交BD于点O,连结OQ.因为O是AC中点,
Q是PC的中点,所以OQ为△PAC中位线.所以OQ//PA. 7分
因为PA![]() 平面BDQ,OQ
平面BDQ,OQ![]() 平面BDQ.所以PA//平面BDQ. 9分
平面BDQ.所以PA//平面BDQ. 9分
(3)设四棱锥P-BCDE,Q-ABCD的分别为![]() ,
,![]() ,所以VP-BCDE=
,所以VP-BCDE=![]() SBCDE
SBCDE![]() ,VQ-ABCD=
,VQ-ABCD=![]() SABCD
SABCD![]() . 10分
. 10分
因为VP-BCDE=2VQ-ABCD,且底面积SBCDE=![]() SABCD. 12分
SABCD. 12分
所以![]() ,因为
,因为![]() ,所以
,所以![]() . 14分
. 14分

 名校课堂系列答案
名校课堂系列答案【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中恰有1名男生的概率是多少?
(3)是否有![]() 把握认为学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
把握认为学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
附:参考数据:
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
![]() ,其中
,其中![]()
