题目内容
f(x)=-cos2x-4tsin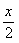 cos
cos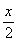 +4t3+t2-3t+4,x∈R,其中|t|≤1,将f(x)的最小值记为g(t)。
+4t3+t2-3t+4,x∈R,其中|t|≤1,将f(x)的最小值记为g(t)。
(1)求g(t)的表达式;
(2)讨论g(t)在区间(-1,1)内的单调性并求极值。
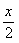 cos
cos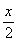 +4t3+t2-3t+4,x∈R,其中|t|≤1,将f(x)的最小值记为g(t)。
+4t3+t2-3t+4,x∈R,其中|t|≤1,将f(x)的最小值记为g(t)。(1)求g(t)的表达式;
(2)讨论g(t)在区间(-1,1)内的单调性并求极值。
解:(1)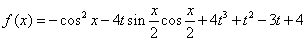
=sin2x-1-2tsinx+4t3+t2-3t+4
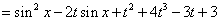
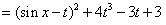
由于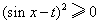 ,
,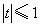 ,故当
,故当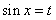 时,
时,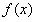 达到其最小值g(t),
达到其最小值g(t),
即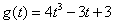 。
。
(2)我们有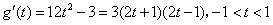
列表如下:
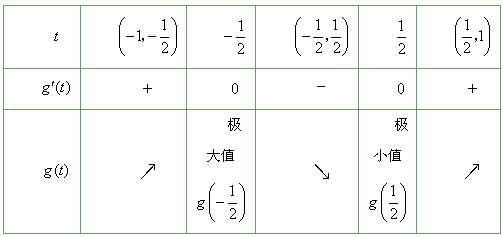
由此可见,g(t)在区间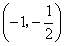 和
和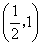 单调增加,
单调增加,
在区间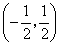 单调减小,极小值为
单调减小,极小值为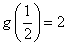 ,极大值为
,极大值为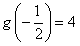 。
。
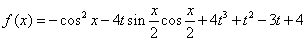
=sin2x-1-2tsinx+4t3+t2-3t+4
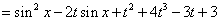
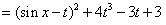
由于
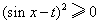 ,
,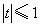 ,故当
,故当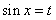 时,
时,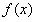 达到其最小值g(t),
达到其最小值g(t),即
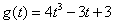 。
。(2)我们有
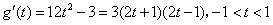
列表如下:

由此可见,g(t)在区间
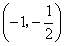 和
和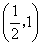 单调增加,
单调增加,在区间
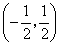 单调减小,极小值为
单调减小,极小值为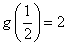 ,极大值为
,极大值为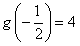 。
。
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目