题目内容
1.在四棱锥P-ABCD中,四条侧棱长均为2,底面ABCD为正方形,E为PC的中点,且∠BED=90°,若该四棱锥的所有顶点都在同一球面上,则该球的表面积是( )| A. | $\frac{16}{3}π$ | B. | $\frac{16}{9}π$ | C. | $\frac{4}{3}π$ | D. | π |
分析 设四棱锥P-ABCD底面棱长为x,则BE=DE=x,根据相似三角形的性质,求出x值,进而求出棱锥的底面的外接圆半径和高,进而求出棱锥的外接球半径,可得答案.
解答 解:设四棱锥P-ABCD底面棱长为x,
∵E为PC的中点,且∠BED=90°,
则BE=DE=x,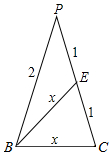
则$\frac{x}{1}=\frac{2}{x}$,解得:x=$\sqrt{2}$,
则正方形ABCD的外接圆半径r=1,
棱锥的高h=$\sqrt{3}$,
设棱锥外接球的半径为R,
则${R}^{2}=(\sqrt{3}-R)^{2}+1$,
解得:R=$\frac{2}{\sqrt{3}}$,
故棱锥的外接球的表面积S=4πR2=$\frac{16}{3}π$,
故选:A
点评 本题考查四棱锥的外接球体积,考查学生的计算能力,确定四棱锥的外接球的半径是关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
13.已知$\sqrt{2+\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$,$\sqrt{3+\frac{3}{8}}$=3$\sqrt{\frac{3}{8}}$,$\sqrt{4+\frac{4}{15}}$=4$\sqrt{\frac{4}{15}}$,…,若$\sqrt{7+\frac{a}{b}}=7\sqrt{\frac{a}{b}}$(a,b∈R),则( )
| A. | a=7,b=35 | B. | a=7,b=48 | C. | a=6,b=35 | D. | a=6,b=48 |