题目内容
11．已知圆C的方程为（x-3）2+y2=4，定点A（-3，0），求过定点A且和圆C外切的动圆圆心P的轨迹方程．分析 由题意画出图形，利用圆心距与半径的关系可得|PC|=|PA|+2，即|PC|-|PA|=2，从而说明点P的轨迹是以A，C为焦点，2为实轴长的双曲线的左支，则答案可求．
解答 解：∵圆P与圆C外切，如图，
∴|PC|=|PA|+2，即|PC|-|PA|=2，
∵0＜|PC|-|PA|＜|AC|，
∴由双曲线的定义，点P的轨迹是以A，C为焦点，2为实轴长的双曲线的左支，其中a=1，c=3，
∴b2=c2-a2=9-1=8．
故所求轨方程为x2-$\frac{y2}{8}$=1（x＜0）．
点评 本题考查轨迹方程的求法，考查圆与圆的位置关系的应用，考查双曲线的定义，是中档题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
2．下列函数中，既是奇函数，又在（1，+∞）上递增的是（ ）
| A． | y=x3-6x | B． | y=x2-2x | C． | y=sinx | D． | y=x3-3x |
19．若函数f（x）的定义域为（-4，4），函数f（2x）的定义域为集合A，集合B={x|x2-x+a-a2＜0}，其中a＜0．
（1）若A∪B=B，求a的取值范围；
（2）若A∩B=B，求a的取值范围．
（1）若A∪B=B，求a的取值范围；
（2）若A∩B=B，求a的取值范围．
6．集合A={x|x-4≥0}，B={x|y=log2（x-2）≤2}，则（∁RA）∩B=（ ）
| A． | {x|2＜x≤4} | B． | {x|2＜x＜4} | C． | {x|2≤x＜4} | D． | {x|2≤x≤4} |
16．
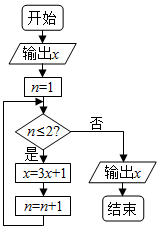从1，2，3，4，5，6，7，8中随机取出一个数为x，执行如图所示的程序框图，则输出的x不小于40的概率为（ ）
从1，2，3，4，5，6，7，8中随机取出一个数为x，执行如图所示的程序框图，则输出的x不小于40的概率为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{5}{8}$ | C． | $\frac{7}{8}$ | D． | $\frac{1}{2}$ |
3．从$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{n}=1$（m，n∈{-1，2，3}）所表示的圆锥曲线（椭圆、双曲线）方程中任取一个，则此方程是焦点在x轴上的双曲线方程的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{4}{7}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
20．从一批苹果中，随机抽取50个，其重量（单位：克）的频数分布表如下：
（I）用分层抽样的方法从重量在[80，85）和[90，95）的苹果中共抽取5个，其中重量在[90，85）的有几个？
（Ⅱ）在（I）中抽出的5个苹果中，任取2个，求重量在[80，85）和[90，95）中各有1个的概率．
| 分组（重量） | [80，85） | [85，90） | [90，95） | [95，100） |
| 频数（个） | 5 | 10 | 20 | 15 |
（Ⅱ）在（I）中抽出的5个苹果中，任取2个，求重量在[80，85）和[90，95）中各有1个的概率．
1．在四棱锥P-ABCD中，四条侧棱长均为2，底面ABCD为正方形，E为PC的中点，且∠BED=90°，若该四棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）
| A． | $\frac{16}{3}π$ | B． | $\frac{16}{9}π$ | C． | $\frac{4}{3}π$ | D． | π |