题目内容
4.在△ABC中,AB=5,AC=6,点P是△ABC的外接圆圆心,则$\overrightarrow{AP}$•$\overrightarrow{B{C}_{\;}}$=$\frac{11}{2}$.分析 设外接圆的半径为r,由向量的三角形法则,以及向量的数量积的定义,结合等腰三角形的性质,即可得到.设外接圆的半径为r,由向量的三角形法则,以及向量的数量积的定义,结合等腰三角形的性质,即可得到.
解答 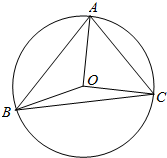 解:设外接圆的半径为r,
解:设外接圆的半径为r,
∴$\overrightarrow{AP}$•$\overrightarrow{B{C}_{\;}}$=$\overrightarrow{AP}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\overrightarrow{AP}$•$\overrightarrow{AC}$-$\overrightarrow{AP}$•$\overrightarrow{AB}$
=r•6•cos∠OAC-r•5•cos∠OAB,
=6×$\frac{6}{2}$-5×$\frac{5}{2}$=$\frac{11}{2}$,
故选:$\frac{11}{2}$.
点评 本题考查向量的数量积的定义和性质,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
8.函数y=2sin($\frac{π}{3}-\frac{x}{3}$)的单调递增区间是( )
| A. | [-$\frac{π}{2}$+2kπ,$\frac{π}{2}$+2kπ](k∈Z) | B. | [$\frac{π}{2}+2kπ$,$\frac{3}{2}$π+2kπ](k∈Z) | ||
| C. | [$\frac{5π}{2}$+6kπ,$\frac{11π}{2}$+6kπ](k∈Z) | D. | [-$\frac{π}{2}$+6kπ,$\frac{5}{2}$π+6kπ](k∈Z) |
9.已知cosα=m,0<|m|<1,且tanα=$\frac{\sqrt{1-{m}^{2}}}{m}$,则角α的终边在( )
| A. | 第一或第二象限 | B. | 第三或第四象限 | C. | 第一或第四象限 | D. | 第二或第三象限 |
6.设集合M={x|x=$\frac{kπ+π}{2}$-$\frac{π}{4}$,k∈Z},N={x|x=$\frac{kπ}{4}$+$\frac{π}{2}$,k∈Z},则( )
| A. | M=N | B. | M?N | C. | M⊆N | D. | M?N |
13.已知复数z=$\sqrt{2}$-3i,则复数的模|z|是( )
| A. | 5 | B. | 8 | C. | 6 | D. | $\sqrt{11}$ |