题目内容
14.设x,y满足约束条件$\left\{\begin{array}{l}1≤x≤3\\-1≤x-y≤0\end{array}\right.$,则z=x-2y的取值范围为[-5,-1].分析 由约束条件作出可行域,联立方程组求出最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}1≤x≤3\\-1≤x-y≤0\end{array}\right.$作出可行域如图,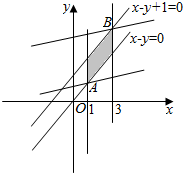
联立$\left\{\begin{array}{l}{x=1}\\{x-y=0}\end{array}\right.$,解得A(1,1),
联立$\left\{\begin{array}{l}{x=3}\\{x-y+1=0}\end{array}\right.$,解得B(3,4),
由图可知,当目标函数z=x-2y过A时,z有最大值为-1;
当目标函数z=x-2y过B时,z有最小值为-5.
故答案为:[-5,-1].
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
4.在△ABC中,AB=5,AC=6,点P是△ABC的外接圆圆心,则$\overrightarrow{AP}$•$\overrightarrow{B{C}_{\;}}$=$\frac{11}{2}$.
5.已知复数z=i,则$\frac{1}{z+1}$的虚部为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}i$ | D. | $-\frac{1}{2}i$ |
2.以圆x2+4x+y2=0的圆心为圆心,半径为3的圆的方程( )
| A. | (x-2)2+y2=3 | B. | (x-2)2+y2=9 | C. | (x+2)2+y2=3 | D. | (x+2)2+y2=9 |
9.函数f(x)=$\sqrt{tanx-1}$的定义域是( )
| A. | $[{\frac{π}{4}+kπ,+∞}),k∈Z$ | B. | $[{\frac{π}{4}+kπ,\frac{π}{2}+kπ}),k∈Z$ | C. | $[{\frac{π}{4}+kπ,\frac{π}{2}+kπ}]$,k∈Z | D. | $[{\frac{π}{4},\frac{π}{2}})$ |
19.已知函数f(x)的定义域为(-∞,0),其导函数为f′(x),且满足2f(x)+f′(x)<0,则不等式f(x+2015)<$\frac{f(-4)}{{e}^{2x+4038}}$的解集为( )
| A. | {x|x>-2019} | B. | {x|x<-2015} | C. | {x|-2019<x<-2015} | D. | {x|-2019<x<0} |
6.函数f(x)=xcosx在点(0,f(0))处的切线斜率是( )
| A. | 0 | B. | -1 | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |