题目内容
11.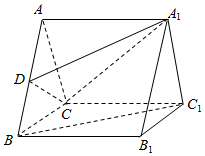 如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形.D为AB中点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形.D为AB中点.(Ⅰ)求证:BC1∥平面A1CD;(Ⅱ)若四边形CBB1C1是正方形,且A1D=$\sqrt{5}$,求多面体CA1C1BD的体积.
分析 (1)取AC1中点E,连结DE,由中位线定理得出DE∥BC1,故而BC1∥平面A1CD;
(2)由勾股定理的逆定理可证明AA1⊥平面ABC,然后利用作差法求出多面体的体积.
解答  解:(I)连结AC1,设AC1∩A1C=E,连结DE,则E是AC1的中点,
解:(I)连结AC1,设AC1∩A1C=E,连结DE,则E是AC1的中点,
∵D是AB的中点,
∴DE∥BC1,又DE?平面A1CD,BC1?平面A1CD,
∴BC1∥平面A1CD.
(II)∵四边形CBB1C1是正方形,△ABC是边长为2的等边三角形,D为AB中点
∴AD=1,AA1=B1B=BC=2,
∴AD2+A1A2=5=A1D2,∴A1A⊥AD,
又∵B1B⊥BC,B1B∥A1A,
∴A1A⊥BC,
又AD?平面ABC,BC?平面ABC,AD∩BC=B,
∴A1A⊥平面ABC,
∵S△ABC=S${\;}_{△{A}_{1}{B}_{1}{C}_{1}}$=$\frac{\sqrt{3}}{4}×{2}^{2}$=$\sqrt{3}$,
∴S△ACD=$\frac{1}{2}{S}_{△ABC}$=$\frac{\sqrt{3}}{2}$.
∴多面体CA1C1BD的体积V=V${\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$-V${\;}_{{A}_{1}-ACD}$-V${\;}_{B-{A}_{1}{B}_{1}{C}_{1}}$=SABC•AA1-$\frac{1}{3}$S△ACD•AA1-$\frac{1}{3}$S${\;}_{△{A}_{1}{B}_{1}{C}_{1}}$•BB1
=$\sqrt{3}×2$-$\frac{1}{3}×\frac{\sqrt{3}}{2}×2$-$\frac{1}{3}×\sqrt{3}×2$=$\sqrt{3}$.
∴多面体CA1C1BD的体积为$\sqrt{3}$.
点评 本题考查了线面平行的判定,多面体的体积计算,属于中档题.

| A. | 4 | B. | 2$\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
| A. | $\frac{\sqrt{6}}{3}$ | B. | 2 | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$ |
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\sqrt{5}-1$ | D. | $\sqrt{2}$ |

 如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,CD=BC=$\frac{1}{2}$AB=1,点P为CE中点.
如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,CD=BC=$\frac{1}{2}$AB=1,点P为CE中点.