题目内容
设等差数列{an}的前n项和为Sn,若S3=9,S5=30,则a7+a8+a9=( )
| A、27 | B、36 | C、42 | D、63 |
考点:等差数列的性质
专题:等差数列与等比数列
分析:由已知可得a1和d,可得Sn,而a7+a8+a9=S9-S6,代入计算可得.
解答:
解:设等差数列{an}的公差为d,
则S3=3a1+3d=9,S5=5a1+10d=30,
联立解得a1=0,d=3,
∴Sn=na1+
d=
,
∴a7+a8+a9=S9-S6=108-45=63,
故选:D.
则S3=3a1+3d=9,S5=5a1+10d=30,
联立解得a1=0,d=3,
∴Sn=na1+
| n(n-1) |
| 2 |
| 3n(n-1) |
| 2 |
∴a7+a8+a9=S9-S6=108-45=63,
故选:D.
点评:本题考查等差数列的性质和求和公式,属基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
设m∈R,i是虚数单位,则“m=1”是“复数m2-m+mi为纯虚数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设全集U=R,集合A={x|0≤x≤2},B={y|1≤y≤3},则(∁UA)∩B=( )
| A、(2,3] |
| B、(-∞,1]∪(2,+∞) |
| C、[1,2) |
| D、(-∞,0)∪[1,+∞) |
已知x与y之间的一组数据如表所示,则x与y的回归直线必过点( )
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A、(2,2) |
| B、(1.5,0) |
| C、(1,2) |
| D、(1.5,4) |
在区间[0,π]内随机取两个数分别记为a、b,则使得函数f(x)=x2+2ax-b2+π有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
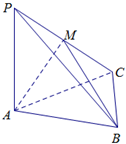 如图,底面是正三角形的三棱锥P-ABC中,PA⊥底面ABC,M为PC中点,且PA=AB,其中下列四个命题:
如图,底面是正三角形的三棱锥P-ABC中,PA⊥底面ABC,M为PC中点,且PA=AB,其中下列四个命题: