题目内容
15.在平面直角坐标系xOy中,已知四边形ABCD是平行四边形,$\overrightarrow{AB}$=(3,1),$\overrightarrow{AD}$=(2,-2),则$\overrightarrow{AC}•\overrightarrow{BD}$( )| A. | 2 | B. | -2 | C. | -10 | D. | 10 |
分析 求出$\overrightarrow{AC},\overrightarrow{BD}$的坐标,再计算数量积.
解答 解:$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$=(5,-1),$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}$=(-1,-3).
∴$\overrightarrow{AC}•\overrightarrow{BD}$=5×(-1)+(-1)×(-3)=-2.
故选B.
点评 本题考查了平面向量的坐标运算,数量级运算,属于基础题.

练习册系列答案
相关题目
6.已知圆x2+y2=17在点(1,4)处的切线与幂函数f(x)的图象在点A(1,f(1))处的切线垂直,且不等式$\frac{f(x)}{x}$>ax2+x在(1,2)上能成立,则实数a的取值范围为( )
| A. | [0,+∞) | B. | ($\frac{35}{6}$,+∞) | C. | (-∞,0] | D. | (-∞,$\frac{3}{2}$) |
20.已知f(x)=cosx•cos2x•cos4x,若f(α)=$\frac{1}{8}$,则角α不可能等于( )
| A. | $\frac{π}{9}$ | B. | $\frac{2π}{9}$ | C. | $\frac{2π}{7}$ | D. | $\frac{4π}{7}$ |
7.下列表述正确的是( )
| A. | 过平面β外一点可以作无数条直线与平面β平行 | |
| B. | 过直线l外一点可作无数条直线平行于l | |
| C. | 垂直于两条异面直线的空间直线只有一条 | |
| D. | 空间三个平面最多把空间分成七部分 |
9.(普通中学做)已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)以及双曲线C2:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线将第一象限三等分,则C1,C2的离心率之积为( )
| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\frac{4}{3}$或4 | C. | $\frac{4}{3}$ | D. | 4 |
10.已知F1(-1,0),F2(1,0)是椭圆C1与双曲线C2共同的焦点,椭圆的一个短轴端点为B,直线F1B与双曲线的一条渐近线平行,椭圆C1与双曲线C2的离心率分别为e1,e2,则e1+e2取值范围为( )
| A. | [2,+∞) | B. | [4,+∞) | C. | (4,+∞) | D. | (2,+∞) |
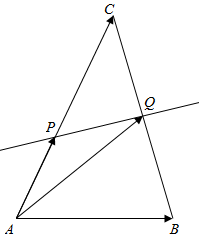 如图,已知△ABC的边BC的垂直平分线交AC于点P,交BC于点Q,若|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=5,则($\overrightarrow{AP}$+$\overrightarrow{AQ}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)的值为-16.
如图,已知△ABC的边BC的垂直平分线交AC于点P,交BC于点Q,若|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=5,则($\overrightarrow{AP}$+$\overrightarrow{AQ}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)的值为-16.