题目内容
4.已知实数a、b常数,若函数y=$\frac{a|x-1|}{x+2}$+be2x+1的图象在切点(0,$\frac{1}{2}$)处的切线方程为3x+4y-2=0,y=$\frac{a|x-1|}{x+2}$+be2x+1与y=k(x-1)3的图象有三个公共点,则实数k的取值范围是(-∞,-$\frac{1}{4}$)∪(0,+∞).分析 求函数的导数,利用导数的几何意义求出a,b的值,利用数形结合判断两个函数的交点个数进行求解即可.
解答 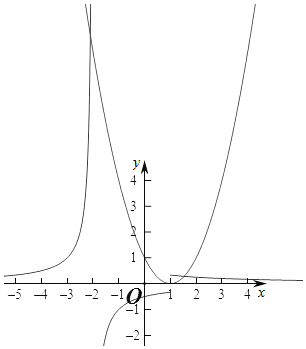 解:当x<1时,函数y=$\frac{a|x-1|}{x+2}$+be2x+1=$\frac{a(1-x)}{x+2}$+be2x+1,
解:当x<1时,函数y=$\frac{a|x-1|}{x+2}$+be2x+1=$\frac{a(1-x)}{x+2}$+be2x+1,
则函数的导数f′(x)=$\frac{-3a}{(x+2)^{2}}$+2be2x+1,
∵若函数y=y=$\frac{a|x-1|}{x+2}$+be2x+1的图象在切点(0,$\frac{1}{2}$)处的切线方程为3x+4y-2=0,
∴f(0)=$\frac{1}{2}$,且f′(0)=-$\frac{3}{4}$,
即$\frac{1}{2}$a+be=$\frac{1}{2}$,-$\frac{3}{4}$a+2be=-$\frac{3}{4}$,得a=1,b=0,
即y=$\frac{a|x-1|}{x+2}$+be2x+1=$\frac{|x-1|}{x+2}$,
由$\frac{|x-1|}{x+2}$=k(x-1)3得当x=1时,方程成立,
当x≠1时,若x>1得$\frac{x-1}{x+2}$=k(x-1)3得$\frac{1}{x+2}$=k(x-1)2,
若x<1得-$\frac{x-1}{x+2}$=k(x-1)3得-$\frac{1}{x+2}$=k(x-1)2,
若k=0,则两个方程无解,
若k>0时,作出对应函数的图象如右图:
此时满足当x>1时,有一个交点,
当x<1时,有一个交点,
此时满足两个函数共有3个交点.
若k<0时,作出对应函数的图象如图: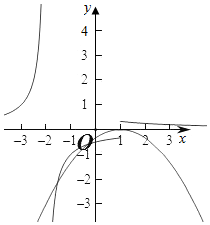
此时满足当x>1时,没有交点,
当x<1时,则需要有2个交点,
由-$\frac{1}{x+2}$=k(x-1)2,
得k(x+2)(x-1)2+1=0,x<1,
设g(x)=k(x+2)(x-1)2+1,
则g′(x)=3k(x-1)(x+1),x<1,k<0,
由g′(x)=0,x=-1,
当x<-1时,g′(x)<0,
当-1<x<1时,g′(x)>0,
即当x=-1函数取得极小值g(-1)=4k+1,
要使当x<1时,则g(x)要有2个交点,
则极小值g(-1)=4k+1<0,得k<-$\frac{1}{4}$,
此时满足两个函数共有3个交点.
综上k的取值范围是k>0或k<0,
故答案为:(-∞,-$\frac{1}{4}$)∪(0,+∞).
点评 本题主要考查函数与方程的应用,根据导数的几何意义求出a,b的值,利用数形结合作出两个函数的图象,利用数形结合是解决本题的关键.

| A. | 有极大值,无极小值 | B. | 有极小值,无极大值 | ||
| C. | 既有极大值又有极小值 | D. | 既无极大值也无极小值 |
| A. | {x|-2019<x<0} | B. | {x|x<-2019} | C. | {x|-2019<x<-2015} | D. | {x|-2011<x<0} |