题目内容
 如图,椭圆
如图,椭圆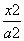 +
+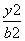 =1(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0).已知点M
=1(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0).已知点M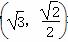 在椭圆上,
在椭圆上,
且点M到两焦点距离之和为4.
(1)求椭圆的方程;
(2)设与MO(O为坐标原点)垂直的直线交椭圆于A,B(A,B不重合),求 的取值范围.
的取值范围.
解 (1)∵2a=4,∴a=2,
又M 在椭圆上,
在椭圆上,
∴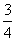 +
+ =1,解得b2=2,
=1,解得b2=2,
∴所求椭圆方程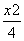 +
+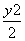 =1.
=1.
(2)由题意知kMO= ,∴kAB=-
,∴kAB=-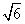 .
.
设直线AB的方程为y=-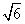 x+m,
x+m,
联立方程组
消去y,得13x2-4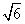 mx+2m2-4=0,
mx+2m2-4=0,
Δ=(-4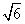 m)2-4×13×(2m2-4)=8(12m2-13m2+26)>0,
m)2-4×13×(2m2-4)=8(12m2-13m2+26)>0,
∴m2<26,设A(x1,y1),B(x2,y2),
由根与系数的关系得x1+x2= ,x1x2=
,x1x2= ,
,
则 =x1x2+y1y2=7x1x2-
=x1x2+y1y2=7x1x2-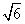 m(x1+x2)+m2=
m(x1+x2)+m2= ∈
∈ .
.
∴ 的取值范围是
的取值范围是 .
.

练习册系列答案
相关题目
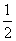 ,b=-4 B.k=-
,b=-4 B.k=-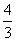 a.
a.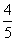 ,则C的离心率为( ).
,则C的离心率为( ). A.
A.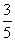 B.
B.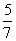 C.
C.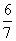
 -
- =1上的一点P到它的右焦点的距离为8,则点P到它的左焦点的距离是 ( ).
=1上的一点P到它的右焦点的距离为8,则点P到它的左焦点的距离是 ( ).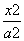 -
-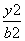 =1(a>0,b>0)的两个焦点.若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为________.
=1(a>0,b>0)的两个焦点.若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为________.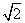 ,2) C.(
,2) C.(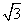 ,2) D.(2,3)
,2) D.(2,3)