题目内容
(本小题满分12分)
已知函数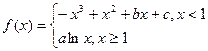
 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点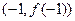 处的切线的斜率是
处的切线的斜率是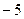 .
.
(Ⅰ)求实数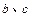 的值;
的值;
(Ⅱ)求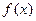 在区间
在区间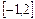 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数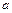 ,曲线
,曲线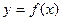 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得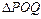 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在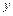 轴上?说明理由。
轴上?说明理由。
解:(Ⅰ)当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①当 时,
时, ,
,
令 得
得
当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
又

0 



— 0 + 0 — 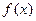
 单调递减
单调递减极小值 单调递增 极大值  单调递减
单调递减 ,
, ,
, 。∴
。∴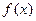 在
在 上的最大值为2.
上的最大值为2.
②当 时,
时,  .当
.当 时,
时,  ,
,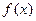 最大值为0
最大值为0
解析

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 、
、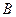 两点的距离为
两点的距离为 海里,
海里,
 处,甲船自
处,甲船自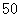 海里/小时的速度向
海里/小时的速度向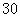 海里/小时的速度沿方位角
海里/小时的速度沿方位角 方向航行。问航行几小时两船之
方向航行。问航行几小时两船之 间的距离最短?
间的距离最短?
 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取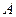 和
和 两点,现测得
两点,现测得 ,
,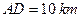 ,
,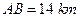 ,
, ,
, ,求两景点
,求两景点

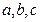 分别为三个内角A、B、C所对的边,
分别为三个内角A、B、C所对的边,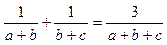 。 (13分)
。 (13分)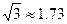 )
)
 12分)
12分) 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为 ,已知
,已知

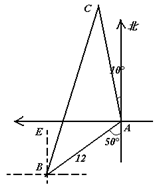
 个与水平面垂直的平面内,B,D为两岛上的两座
个与水平面垂直的平面内,B,D为两岛上的两座 灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为
灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为 ,
,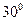 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为 ,AC=0.1km。
,AC=0.1km。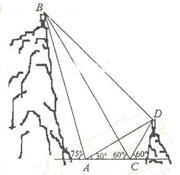

 在△ABC中,角A,B,C所对的边分别为a,b,c,
在△ABC中,角A,B,C所对的边分别为a,b,c,
 的值;
的值; 的值.
的值.