题目内容

9．设复数z=（m2-m-2）+（m2+3m+2）i，试求m为何值时，
（Ⅰ）z为实数；
（Ⅱ）z为纯虚数．

分析 （I）利用复数为实数的充要条件即可得出．
（II）利用纯虚数的定义即可得出．

解答 解：（I）复数z=（m2-m-2）+（m2+3m+2）i为实数，则m2+3m+2=0，解得m=-1或m=-2；
（II）复数z=（m2-m-2）+（m2+3m+2）i为纯虚数，则m2-m-2=0，m2+3m+2≠0，解得m=2．

点评 本题考查了复数为实数的充要条件、纯虚数的定义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
2．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，且点（1，$\frac{3}{2}$）在椭圆E上．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设动直线l：y=kx+m（k，m∈R）与椭圆E只有一个公共点P．
（1）用实数k，m表示点P的坐标；
（2）若动直线l与直线x=4相交于点Q，问：在x轴上是否存在定点M，使得MP⊥MQ？若存在，求出定点M的坐标；若不存在，请说明理由．
20．将函数$y=2sin（3x-\frac{π}{2}）$的图象向左平移φ（φ＞0）个单位后，所得到的图象对应的函数为奇函数，则φ的最小值为$\frac{π}{6}$．
17．已知两条坐标轴是圆C1：（x-1）2+（y-1）2=1与圆C2的公切线，且两圆的圆心距是3$\sqrt{2}$，求圆C2的方程．
4．某地举行公车拍卖会，轿车拍卖成交了4辆，成交价分别为5元，x万元，7万元，9万元；货车拍卖成交了2辆，成交价分别为7万元，8万元．总平均成交价格为7万元．
（1）求该场拍卖会成交价格的中位数；
（2）某人拍得两辆车，求拍得轿车、货车各一辆且总成交价格不超过14万元的概率．
14．计算下列各式的值
（1）${8}^{\frac{2}{3}}$•（$\frac{1}{3}$）3•$（\frac{16}{81}）^{-\frac{3}{4}}$
（2）log535+$2lo{g}_{\frac{1}{2}}\sqrt{2}-lo{g}_{5}\frac{1}{50}-lo{g}_{5}14$．
1．设集合A={x|y=$\sqrt{x-1}$}，集合B={x|2x-x2＞0}，则（∁RA）∩B等于（
A．（0，2）B．[1，2）C．（0，1）D．∅
18．圆x2+y2-2x-2y+1=0上点到直线x+y-4=0的最大距离与最小距离的差为（　　）
A．$\sqrt{2}$B．$\sqrt{2}+1$C．2D．$\sqrt{2}-1$
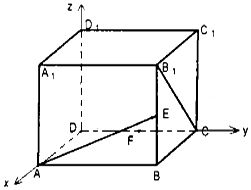19．在正方体ABCD-A1B1C1D1中，如图E、F分别是BB1，CD的中点，
（1）求证：D1F⊥AE；
（2）求直线EF与CB1所成角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网