题目内容
5．已知实数x，y满足3x2+2y2=6x，则x2+y2的最大值是（ ）| A． | $\frac{9}{2}$ | B． | 4 | C． | 5 | D． | 2 |
分析 化二元为一元，注意确定变量的范围，转化为二次函数的最值，利用配方法可求结论．
解答 解：∵3x2+2y2=6x，∴y2=-$\frac{3}{2}$x2+3x，
由y2=-$\frac{3}{2}$x2+3x≥0，
可得0≤x≤2，
又x2+y2=x2-$\frac{3}{2}$x2+3x=-$\frac{1}{2}$x2+3x=-$\frac{1}{2}$（x-3）2+$\frac{9}{2}$，
∵0≤x≤2，
∴x=2时，x2+y2的最大值为4．
故选：B．
点评 本题考查最值问题，考查学生转化问题的能力，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
6．
如图所示，正方体ABCD-A1B1C1D1的棱长为a，M，N分别为A1B和AC上的点，A1M=AN=$\frac{a}{3}$，则MN与平面BB1C1C的位置关系为（ ）
如图所示，正方体ABCD-A1B1C1D1的棱长为a，M，N分别为A1B和AC上的点，A1M=AN=$\frac{a}{3}$，则MN与平面BB1C1C的位置关系为（ ）| A． | 相交 | B． | 平行 | C． | 垂直 | D． | 不能确定 |
3．数学表达式$\sqrt{x}$在程序中表示为（ ）
| A． | ABS（x） | B． | SQR（x） | C． | RND（x） | D． | INT（x） |
如图，等腰三角形ABC中，E为底边BC的中点，△AEC沿AE折叠，将点C折到点P的位置，使二面角P-AE-B为60°，设点P在平面ABE上的射影为H．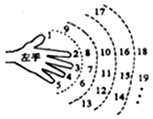
某小朋友按如下规则练习数数，1大拇指，2食指，3中指，4无名指，5小指，6无名指，7中指，8食指，9大拇指，10食指，…，一直数到2017时，对应的指头是大拇指．