题目内容
6.若0<x<1,则下列结论正确的是( )| A. | $\sqrt{x}$>2x>lgx | B. | 2x$>lgx>\sqrt{x}$ | C. | 2x$>\sqrt{x}$>lgx | D. | lgx$>\sqrt{x}$>2x |
分析 【解法一】根据题意,用特殊值法,取x=$\frac{1}{2}$,代入化简、比较大小即可.
【解法二】利用指数函数、对数函数与幂函数的图象与性质,也可以比较大小.
解答 解:【解法一】∵0<x<1,不妨取x=$\frac{1}{2}$,
则$\sqrt{x}$=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,2x=${2}^{\frac{1}{2}}$=$\sqrt{2}$,lgx=lg$\frac{1}{2}$=-lg2,
且$\sqrt{2}$>$\frac{\sqrt{2}}{2}$>-lg2,
∴2x>$\sqrt{x}$>lgx.
【解法二】0<x<1时,0<$\sqrt{x}$<1,
2x>20=1,
lgx<lg1=0;
∴2x>$\sqrt{x}$>lgx.
故选:C.
点评 本题考查了利用对数函数的图象与性质比较大小的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知x,y满足(x-1)2+y2=16,则x2+y2的最大值为( )
| A. | 3 | B. | 5 | C. | 9 | D. | 25 |
14.已知a=0.71.3,b=30.2,c=log0.25,则a、b、c之间的大小关系为( )
| A. | a<c<b | B. | c<b<a | C. | b<c<a | D. | c<a<b |
11.函数f(x)=-2x2+ax+1在($\frac{1}{2},+∞$)是减函数,则a的取值范围是( )
| A. | ($-∞,\frac{1}{2}$) | B. | (-∞,2] | C. | [4,+∞) | D. | (-∞,-2] |
16.${(x-\frac{1}{x})^6}$展开式中的常数项为( )
| A. | 15 | B. | 20 | C. | -1 | D. | -20 |
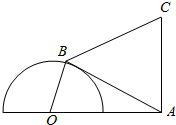 如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC,设∠AOB=α.问:当α取何值时,四边形OACB面积最大?
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC,设∠AOB=α.问:当α取何值时,四边形OACB面积最大?