题目内容
9.若不等式组$\left\{\begin{array}{l}{x≥0}\\{x+3y≥4}\\{3x+y≤4}\end{array}\right.$,所表示的平面区域被直线y=kx+$\frac{4}{3}$分为面积相等的两部分,则k的值是$\frac{7}{3}$.分析 先根据约束条件,画出可行域,求出可行域顶点的坐标,再利用几何意义求面积即可
解答 解:不等式组$\left\{\begin{array}{l}{x≥0}\\{x+3y≥4}\\{3x+y≤4}\end{array}\right.$,所表示的平面区域如图示: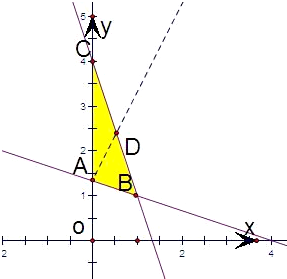
由图可知,直线y=kx+$\frac{4}{3}$恒经过点A(0,$\frac{4}{3}$),当直线y=kx+$\frac{4}{3}$再经过BC的中点D($\frac{1}{2}$,$\frac{5}{2}$)时,平面区域被直线y=kx+$\frac{4}{3}$分为面积相等的两部分,
当x=$\frac{1}{2}$,y=$\frac{5}{2}$时,代入直线y=kx+$\frac{4}{3}$的方程得:
k=$\frac{7}{3}$;
故答案为:$\frac{7}{3}$
点评 本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.

练习册系列答案
相关题目
19.已知F1、F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P是该双曲线上的任意一点,若△PF1F2的内切圆半径为r,则r的取值范围是( )
| A. | (0,a) | B. | (0,b) | C. | (0,$\sqrt{{a}^{2}+{b}^{2}}$) | D. | (0,$\sqrt{ab}$) |
4.已知函数f(x)的图象是连续不断的,有如下的x,f(x)对应值表:
那么函数f(x)在区间[1,6]上的零点至少有( )
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(x) | 123.5 | 21.5 | -7.82 | 11.57 | -53.7 | -126.7 | -129.6 |
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
1.某农户计划种植黄瓜和冬瓜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜与冬瓜的产量、成本和售价如表:
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜与冬瓜的种植面积(单位:亩)分别为( )
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 冬瓜 | 6吨 | 0.9万元 | 0.3万元 |
| A. | 50,0 | B. | 30,20 | C. | 20,30 | D. | 0,50 |
19.若数列{an}满足a1=$\sqrt{3}$,an+1=[an]+$\frac{1}{\{{a}_{n}\}}$([an]与{an}分别表示an的整数部分与小数部分),则a2016=( )
| A. | 3023+$\sqrt{3}$ | B. | 3023+$\frac{\sqrt{3}-1}{2}$ | C. | 3020+$\sqrt{3}$ | D. | 3020+$\frac{\sqrt{3}-1}{2}$ |
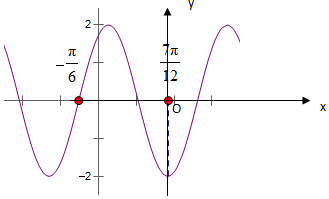 已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.
已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.