题目内容
6．已知圆锥的底面积为3π，高为3，则该圆锥的外接球的表面积为16π．分析 利用射影定理，求出圆锥的外接球的半径，即可求出圆锥的外接球的表面积．
解答 解：设圆锥的底面半径是r，圆锥的外接球的半径为R，则
∵圆锥的底面积为3π，∴r=$\sqrt{3}$，
∴3=3（2R-3），∴R=2，
∴圆锥的外接球的表面积为4π•4=16π．
故答案为16π．
点评 本题考查了圆锥的结构特征，考查学生的计算能力，确定圆锥的外接球的半径是关键，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．已知定义在R上的函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-6ax-1，x≤1}\\{{a}^{x}-7，x＞1}\end{array}\right.$，对任意x1≠x2，都有$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＜0，则实数a的取值范围是（ ）
| A． | （$\frac{1}{3}$，1） | B． | [$\frac{1}{3}$，1） | C． | （0，$\frac{1}{3}$） | D． | （0，$\frac{1}{3}$] |
11．在△ABC中，$∠C=\frac{π}{4}$，AB=2，$AC=\sqrt{6}$，则cosB的值为（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$或$-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{1}{2}$或$-\frac{1}{2}$ |
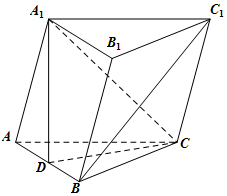如图，三棱柱ABC-A1B1C1中，AC=BC，AB=AA1，∠A1AB=60°，D是AB的中点．
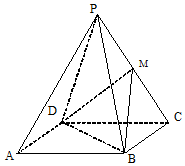已知四棱锥P-ABCD中底面四边形ABCD是正方形，各侧面都是边长为2的正三角形，M是棱PC的中点．建立空间直角坐标系，利用空间向量方法解答以下问题：