题目内容
11.在△ABC中,$∠C=\frac{π}{4}$,AB=2,$AC=\sqrt{6}$,则cosB的值为( )| A. | $\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$或$-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$或$-\frac{1}{2}$ |
分析 根据正弦定理和内角和定理可得答案:
解答 解:由题意:$∠C=\frac{π}{4}$,c=AB=2,b=$AC=\sqrt{6}$,
由正弦定理$\frac{b}{sinB}$=$\frac{c}{sinC}$,则有:sinB=$\frac{\sqrt{6}sin\frac{π}{4}}{2}$=$\frac{\sqrt{3}}{2}$.
∵0<B<π
∴B=$\frac{π}{3}$或$\frac{2π}{3}$.
当B=$\frac{π}{3}$时,则cosB=$\frac{1}{2}$
当B=$\frac{2π}{3}$时,则cosB=$-\frac{1}{2}$.
故选D
点评 本题考查三角形的正弦定理和内角和定理的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
2.已知函数y=f(x)满足f(x+1)=x+3a,且f(a)=3.
(1)求函数f(x)的解析式;
(2)若g(x)=x•f(x)+λf(x)+1在(0,2)上具有单调性,λ<0,求g(λ)的取值范围.
(1)求函数f(x)的解析式;
(2)若g(x)=x•f(x)+λf(x)+1在(0,2)上具有单调性,λ<0,求g(λ)的取值范围.
19.下列函数中,在区间(0,1)上是增函数的是( )
| A. | y=$\frac{1}{x}$ | B. | y=5-2x | C. | y=|x| | D. | y=-2x2+1 |
16.中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中$115.1\frac{4}{6}$寸表示115寸$1\frac{4}{6}$分(1寸=10分).
已知《易经》中记录的冬至晷影长为130.0寸,夏至晷影长为14.8寸,那么《易经》中所记录的惊蛰的晷影长应为82寸.
| 节 气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
| 晷影 长 (寸) | 135.0 | $125.\frac{5}{6}$ | $115.1\frac{4}{6}$ | $105.2\frac{3}{6}$ | $95.3\frac{2}{6}$ | $85.4\frac{2}{6}$ | 75.5 | $66.5\frac{5}{6}$ | $55.6\frac{4}{6}$ | $45.7\frac{3}{6}$ | $35.8\frac{2}{6}$ | $25.9\frac{1}{6}$ | 16.0 |
20.已知O,A,B三地在同一水平面内,A地在O地正东方向2km处,B地在O地正北方向2km处,某测绘队员在A、B之间的直线公路上任选一点C作为测绘点,用测绘仪进行测绘,O地为一磁场,距离其不超过$\sqrt{3}km$的范围内对测绘仪等电子仪器形成干扰,使测量结果不准确,则该测绘队员能够得到准确数据的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $1-\frac{{\sqrt{3}}}{2}$ | D. | $1-\frac{{\sqrt{2}}}{2}$ |
1.从0,1,2,3,4中任选两个不同的数字组成一个两位数,其中偶数的个数是( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
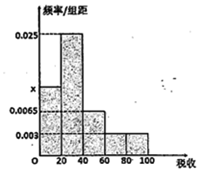 我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]
我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]