题目内容
已知直线C1:
’(t为参数),曲线C2:
(θ为参数).
(1)当α=
时,求C1与C2的交点坐标;
(2)当α变化时,求直线C1与曲线C2相交所得弦长的取值范围.
|
|
(1)当α=
| π |
| 3 |
(2)当α变化时,求直线C1与曲线C2相交所得弦长的取值范围.
考点:参数方程化成普通方程
专题:
分析:(1)当α=
时,直线C1:
’消去参数t可得:y=
x-
,曲线C2:
(θ为参数).消参得:x2+y2=13,联立基础即可得到交点坐标.
(2)直线C1:
’(t为参数),化为y=(x-1)tanα,或x=1,由参数方程可得直线是过点(1,0)的任意直线,然后由圆的几何性质得:
最长弦是直径为,垂直于直径的弦最短即2
,其中d为圆心到直线的距离.
| π |
| 3 |
|
| 3 |
| 3 |
|
(2)直线C1:
|
最长弦是直径为,垂直于直径的弦最短即2
| r2-d2 |
解答:
解:(1)当α=
时,直线C1:
’消去参数t可得:y=
x-
,-------①
曲线C2:
(θ为参数).消参得:x2+y2=13--------②
联立①、②化为2x2-3x-5=0,
解得:
或
,
所以交点坐标分别为(-1,-2
),(
,
).
(2)直线C1:
’(t为参数),化为y=(x-1)tanα,或x=1,
由参数方程可得直线是过点(1,0)的任意直线,然后由圆的几何性质得:
最长弦是直径为2
,垂直于直径的弦最短即2
=7.
∴直线C1与曲线C2相交所得弦长的取值范围是[7,2
].
| π |
| 3 |
|
| 3 |
| 3 |
曲线C2:
|
联立①、②化为2x2-3x-5=0,
解得:
|
|
所以交点坐标分别为(-1,-2
| 3 |
| 5 |
| 2 |
3
| ||
| 2 |
(2)直线C1:
|
由参数方程可得直线是过点(1,0)的任意直线,然后由圆的几何性质得:
最长弦是直径为2
| 13 |
13-(
|
∴直线C1与曲线C2相交所得弦长的取值范围是[7,2
| 13 |
点评:本题考查了把参数方程化为普通方程、直线与曲线的交点、直线与圆的相交弦长问题、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若任取x,y∈(0,1],则点P(x,y)满足y≤x
的概率为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若双曲线
-
=1上一点P对焦点F1,F2的视角为60°,则△F1PF2的面积为( )
| x2 |
| 16 |
| y2 |
| 9 |
A、2
| ||
B、3
| ||
C、6
| ||
D、9
|
根据如图的算法流程图,当输入x的值为3时,输出的结果为( )


| A、5 | B、6 | C、7 | D、8 |
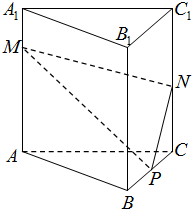 如图,在三棱柱ABC-A1B1C1中,已知侧棱AA1⊥平面ABC,△ABC是边长为2的等边三角形,M是AA1上的一点,AA1=4,A1M=1.P是棱BC上的一点,且由点P沿棱柱侧面经过棱CC1到点M的最短距离为3
如图,在三棱柱ABC-A1B1C1中,已知侧棱AA1⊥平面ABC,△ABC是边长为2的等边三角形,M是AA1上的一点,AA1=4,A1M=1.P是棱BC上的一点,且由点P沿棱柱侧面经过棱CC1到点M的最短距离为3