题目内容
设函数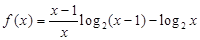
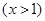 .
.
(I)求函数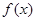 的最小值;
的最小值;
(Ⅱ)若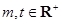 ,且
,且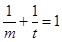 ,求证:
,求证: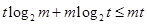 ;
;
(Ⅲ)若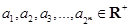 ,且
,且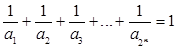 ,
,
求证: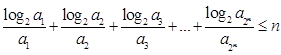 .
.
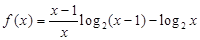
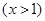 .
.(I)求函数
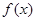 的最小值;
的最小值;(Ⅱ)若
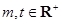 ,且
,且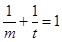 ,求证:
,求证: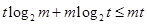 ;
;(Ⅲ)若
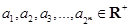 ,且
,且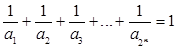 ,
,求证:
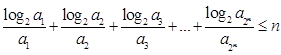 .
.解:(I) ,
,

令 ,得
,得 ,所以
,所以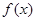 在
在 递减,在
递减,在 递增.
递增.
所以 .
.
(Ⅱ)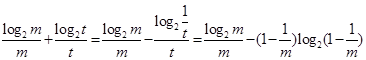


由(I)知当 时,
时, ,
,
又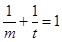 ,
,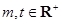 ,∴
,∴
∴ .
.
(Ⅲ)用数学归纳法证明如下:1°当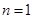 时,由(Ⅱ)可知,不等式成立;
时,由(Ⅱ)可知,不等式成立;
2°假设 (
( )时不等式成立,
)时不等式成立,
即若 ,且
,且 时,
时,
不等式 成立
成立
现需证当 (
( )时不等式也成立,
)时不等式也成立,
即证:若 ,且
,且 时,不等式
时,不等式
 成立.
成立.
证明如下:设 ,则
,则

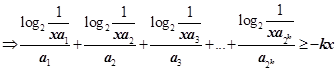
 ......①
......①
同理
 .....②
.....②
由①+②得: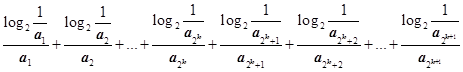

又由(Ⅱ)令 ,则
,则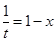 ,其中
,其中 ,
,
则有
∴ ∴
∴

∴当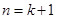 时,原不等式也成立.
时,原不等式也成立.
综上,由1°和2°可知,对任意的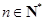 原不等式均成立.
原不等式均成立.
 ,
,
令
 ,得
,得 ,所以
,所以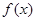 在
在 递减,在
递减,在 递增.
递增.所以
 .
.(Ⅱ)
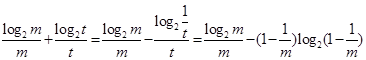


由(I)知当
 时,
时, ,
,又
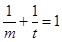 ,
,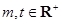 ,∴
,∴
∴
 .
.(Ⅲ)用数学归纳法证明如下:1°当
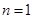 时,由(Ⅱ)可知,不等式成立;
时,由(Ⅱ)可知,不等式成立;2°假设
 (
( )时不等式成立,
)时不等式成立,即若
 ,且
,且 时,
时,不等式
 成立
成立现需证当
 (
( )时不等式也成立,
)时不等式也成立,即证:若
 ,且
,且 时,不等式
时,不等式 成立.
成立.证明如下:设
 ,则
,则

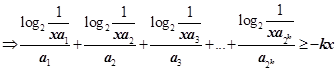
 ......①
......①同理

 .....②
.....②由①+②得:
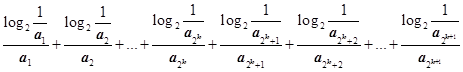

又由(Ⅱ)令
 ,则
,则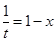 ,其中
,其中 ,
,则有

∴
 ∴
∴

∴当
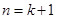 时,原不等式也成立.
时,原不等式也成立.综上,由1°和2°可知,对任意的
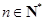 原不等式均成立.
原不等式均成立.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
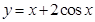 在区间
在区间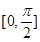 上的最大值是 。
上的最大值是 。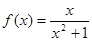
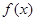 的极大值和极小值,并画出函数
的极大值和极小值,并画出函数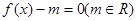 的根的个数问题:
的根的个数问题: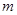 的取值范围
的取值范围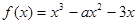
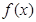 在区间上
在区间上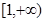 是增函数,求实数
是增函数,求实数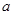 的取值范围;
的取值范围;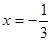 是
是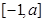 上的最大值和最小值.
上的最大值和最小值.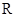 上的函数
上的函数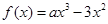 ,其中
,其中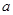 为大于零的常数.
为大于零的常数.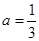 时,令
时,令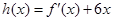 ,
,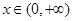 时,
时,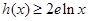 (
(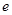 为自然对数的底数);
为自然对数的底数);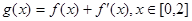 ,在
,在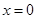 处取得最大值,求
处取得最大值,求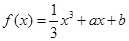 ,
,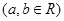 在
在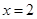 处取得极小值
处取得极小值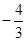 。求a+b的值
。求a+b的值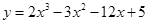 在[0,3]上的最大值、最小值分别是
在[0,3]上的最大值、最小值分别是 在
在 处有极值,则
处有极值,则



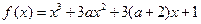 ,既有极大值又有极小值,则
,既有极大值又有极小值,则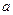 的取值范围是
的取值范围是 