题目内容
 如图:将圆柱的侧面沿母线AA1展开,得到一个长为2π,宽AA1为2的矩形.
如图:将圆柱的侧面沿母线AA1展开,得到一个长为2π,宽AA1为2的矩形.(1)求此圆柱的体积;
(2)由点A拉一根细绳绕圆柱侧面两周到达A1,求绳长的最小值(绳粗忽略不计).
考点:旋转体(圆柱、圆锥、圆台)
专题:计算题,空间位置关系与距离
分析:(1)利用将圆柱的侧面沿母线AA1展开,得到一个长为2π,宽AA1为2的矩形,求出圆柱的底面半径、高,再求出此圆柱的体积;
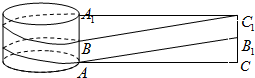
(2)设AA1中点为B,侧面展开图矩形为ACC1A1,CC1中点为B1.则绳长的最小值即为侧面展开图中的AB1+BC1.
(2)设AA1中点为B,侧面展开图矩形为ACC1A1,CC1中点为B1.则绳长的最小值即为侧面展开图中的AB1+BC1.
解答:
 解:(1)设圆柱的底面半径为r,高为h,则2πr=2π,h=2,
解:(1)设圆柱的底面半径为r,高为h,则2πr=2π,h=2,
∴r=1,h=2,---------(2分)
∴V=πr2h=2π--------(5分)
(2)设AA1中点为B,侧面展开图矩形为ACC1A1,CC1中点为B1.则绳长的最小值即为侧面展开图中的AB1+BC1.-------(7分)
AB1=BC1=
.-------(10分)
∴绳长的最小值为2
.-------(12分)
 解:(1)设圆柱的底面半径为r,高为h,则2πr=2π,h=2,
解:(1)设圆柱的底面半径为r,高为h,则2πr=2π,h=2,∴r=1,h=2,---------(2分)
∴V=πr2h=2π--------(5分)
(2)设AA1中点为B,侧面展开图矩形为ACC1A1,CC1中点为B1.则绳长的最小值即为侧面展开图中的AB1+BC1.-------(7分)
AB1=BC1=
| 4π2+1 |
∴绳长的最小值为2
| 4π2+1 |
点评:本题考查棱柱的结构特征,空间想象能力,几何体的展开与折叠,体现了转化(空间问题转化为平面问题,化曲为直)的思想方法.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
设U=R,集合A={x|x>0},B={x∈Z|x2-4≤0},则下列结论正确的是( )
| A、(∁UA)∩B={-2,-1,0} |
| B、(∁UA)∪B=(-∞,0] |
| C、(∁UA)∩B={1,2} |
| D、A∪B=(0,+∞) |
在极坐标系中,点(2,-
)到圆ρ=-2cosθ的圆心的距离为( )
| π |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
曲线y=ex+1在点(0,2)处的切线与直线y=0和x=0围成的三角形面积为( )
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |