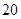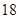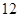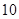题目内容
已知椭圆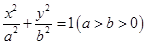 ,
,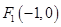 、
、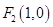 是椭圆的左右焦点,且椭圆经过点
是椭圆的左右焦点,且椭圆经过点 .
.
(1)求该椭圆方程;
(2)过点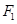 且倾斜角等于
且倾斜角等于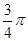 的直线
的直线 ,交椭圆于
,交椭圆于 、
、 两点,求
两点,求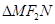 的面积.
的面积.
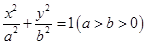 ,
,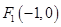 、
、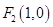 是椭圆的左右焦点,且椭圆经过点
是椭圆的左右焦点,且椭圆经过点 .
.(1)求该椭圆方程;
(2)过点
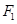 且倾斜角等于
且倾斜角等于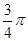 的直线
的直线 ,交椭圆于
,交椭圆于 、
、 两点,求
两点,求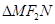 的面积.
的面积.(1)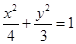 ;(2)
;(2)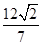 .
.
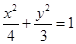 ;(2)
;(2)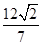 .
.试题分析:(1)求椭圆标准方程,就是要求
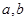 ,也即要找到关于
,也即要找到关于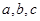 的两个条件,本题中有
的两个条件,本题中有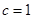 ,又有椭圆过点
,又有椭圆过点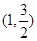 ,把点坐标代入椭圆方程又得到一个关系式,解之即得;(2)本题是直线与椭圆相交问题,如果交点坐标能简单求出,那么我们就求出交点坐标,然后再解题,但一般情况下,这类问题中都含有参数,或者交战坐标很复杂,不易求得,这时我们采取“设而不求”的方法,即设交点为
,把点坐标代入椭圆方程又得到一个关系式,解之即得;(2)本题是直线与椭圆相交问题,如果交点坐标能简单求出,那么我们就求出交点坐标,然后再解题,但一般情况下,这类问题中都含有参数,或者交战坐标很复杂,不易求得,这时我们采取“设而不求”的方法,即设交点为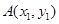 ,
,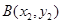 ,在把直线方程代入椭圆(或其他圆锥曲线)方程消去
,在把直线方程代入椭圆(或其他圆锥曲线)方程消去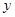 得关于
得关于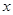 的二次方程,则有
的二次方程,则有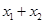 ,
,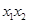 ,则
,则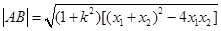 ,本题有
,本题有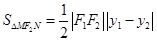 ,由此可求出面积.
,由此可求出面积.(1)
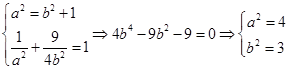 ,则椭圆方程为
,则椭圆方程为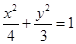 . 6分
. 6分(2)设
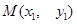 ,
,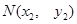 ,直线
,直线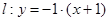 . 8分
. 8分由
 , 10
, 10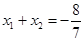 ,
,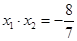
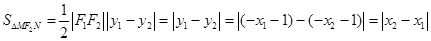
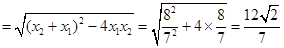 . 14分
. 14分
练习册系列答案
相关题目
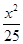 +
+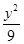 =1的左、右焦点分别是F1、F2,P为椭圆C上的一点,且PF1⊥PF2,则△PF1F2的面积为________.
=1的左、右焦点分别是F1、F2,P为椭圆C上的一点,且PF1⊥PF2,则△PF1F2的面积为________.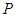 是椭圆
是椭圆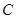 上任一点,点
上任一点,点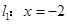 的距离为
的距离为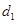 ,到点
,到点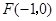 的距离为
的距离为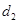 ,且
,且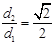 .直线
.直线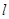 与椭圆
与椭圆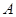 、
、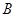 (
(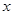 轴上方),且
轴上方),且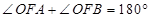 .
.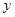 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线 如何变化,直线
如何变化,直线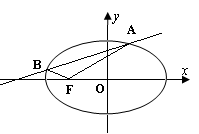
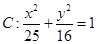 上一点,F为椭圆C的右焦点,若点M满足
上一点,F为椭圆C的右焦点,若点M满足 且
且 ,则
,则 的最小值为( )
的最小值为( )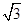
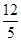
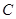 的中心在原点,焦点在
的中心在原点,焦点在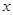 轴上,离心率为
轴上,离心率为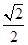 ,它的一个焦点恰好与抛物线
,它的一个焦点恰好与抛物线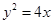 的焦点重合.
的焦点重合. ,过点
,过点 ,若直线
,若直线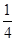 ,直线
,直线 是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.
是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.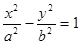 离心率是
离心率是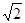 ,过点
,过点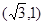 ,且右支上的弦
,且右支上的弦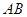 过右焦点
过右焦点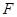 .
.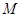 的轨迹E的方程;
的轨迹E的方程; (a>b>0)的左、右焦点,若在直线x=
(a>b>0)的左、右焦点,若在直线x= 上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )



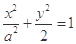 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,则该椭圆的离心率是( )
的焦点重合,则该椭圆的离心率是( )
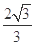
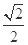

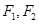 为椭圆
为椭圆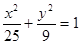 的两个焦点,过
的两个焦点,过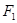 的直线交椭圆于两点,
的直线交椭圆于两点,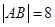 ,
,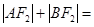 ( )
( )