题目内容
设函数 ,给出下列四个命题:
,给出下列四个命题:
① 时,
时, 是奇函数 ②
是奇函数 ②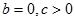 时,方程
时,方程 只有一个实根
只有一个实根
③ 的图象关于
的图象关于 对称 ④方程
对称 ④方程 至多两个实数根
至多两个实数根
其中正确的命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
C
解析试题分析:对于① 时,f(x)=
时,f(x)=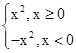 结合图像可知是奇函数,成立。
结合图像可知是奇函数,成立。
对于②因为f(x)=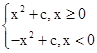 当x≥0时无根,当x<0时,有一根x=-
当x≥0时无根,当x<0时,有一根x=-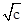 .故当b=0,c>0时,方程f(x)=0只有一个实根;②对.
.故当b=0,c>0时,方程f(x)=0只有一个实根;②对.
对于③设g(x)=x|x|+bx,因为g(-x)=-x|-x|+b(-x)=-g(x),所以g(x)=x|x|+bx关于(0,0)对称,又函数y=f(x)的图象可以由g(x)=x|x|+bx的图象上下平移c个单位得到.故函数y=f(x)的图象关于点(0,c)对称;故③对.
对于④分各种情况来讨论b,c,并求出对应方程的根,就可说明④不成立,故选C.
考点:本试题主要考查了对带绝对值的二次函数的综合考查.
点评:解决该试题的关键是通常带绝对值的函数研究其性质时,要去掉其绝对值符号进行

练习册系列答案
相关题目
设p、q是两上命题,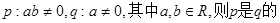 ( )
( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列特称命题中真命题的个数是()
①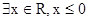
②至少有一个整数,它既不是合数,也不是素数
③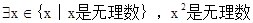
| A.0 | B.1 | C.2 | D.3 |
下列有关命题的说法正确的是
A.命题“若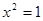 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若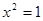 ,则 ,则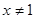 ”; ”; |
B.命题“  ”的否定是“ ”的否定是“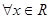 , ,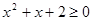 ,”; ,”; |
C.命题“若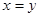 ,则 ,则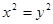 ”的逆否命题是假命题 ; ”的逆否命题是假命题 ; |
D.已知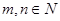 ,命题“若 ,命题“若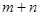 是奇数,则 是奇数,则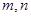 这两个数中一个为奇数,另一个为偶数”的逆命题为假命题. 这两个数中一个为奇数,另一个为偶数”的逆命题为假命题. |
已知 :函数
:函数 与
与 轴有两个交点;
轴有两个交点; :
: ,
, 恒成立.若
恒成立.若 为真,则实数m的取值范围为 ( )
为真,则实数m的取值范围为 ( )
A. | B. |
C. | D. |
设条件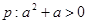 , 条件
, 条件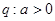 ; 那么
; 那么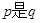 的( )
的( )
| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题正确的是( )
A. | B. |
C. 是 是 的充分不必要条件 的充分不必要条件 | D.若 ,则 ,则 |
若命题“ ”为假,且
”为假,且 为假,则( )
为假,则( )
A.“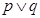 ”为假 ”为假 | B. 假 假 | C. 真 真 | D. 假 假 |
下列说法中,正确的是
A.命题“若 ,则 ,则 ”的逆命题是真命题 ”的逆命题是真命题 |
B.命题“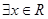 ,使得 ,使得 ”的否定是:“ ”的否定是:“  ,都有 ,都有 或 或 ” ” |
C.命题“ 或 或 ”为真命题,则命题“ ”为真命题,则命题“ ”和命题“ ”和命题“ ”均为真命题 ”均为真命题 |
D.已知 ,则“ ,则“ ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |