Question

设二次函数f(x)＝ax²＋bx＋c，函数F(x)＝f(x)－x的两个零点为m，n(m＜n)．

(1)若m＝－1，n＝2，求不等式F(x)＞0的解集；

(2)若a＞0，且0＜x＜m＜n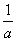＜，比较f(x)与m的大小．

Answer 1

解：(1)由题意知，F(x)＝f(x)－x＝a(x－m)(x－n)，

当m＝－1，n＝2时，不等式F(x)＞0，

即a(x＋1)(x－2)＞0.

那么当a＞0时，不等式F(x)＞0的解集为{x|x＜－1，或x＞2}；

当a＜0时，不等式F(x)＞0 的解集为{x|－1＜x＜2}．

(2)f(x)－m＝a(x－m)(x－n)＋x－m＝

(x－m)(ax－an＋1)，

∵a＞0，且0＜x＜m＜n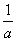＜，∴x－m＜0，

1－an＋ax＞0.

∴f(x)－m＜0，即f(x)＜m.