题目内容
已知点An(n，an)为函数y＝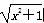
图象上的点，Bn(n，bn)为函数y＝x图象上的点，其中n∈N*，设cn＝a
n－bn，则cn与cn＋1的大小关系为________．
cn＋1<cn
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
开心快乐假期作业暑假作业西安出版社系列答案题目内容
已知点An(n，an)为函数y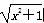＝图象上的点，Bn(n，bn)为函数y＝x图象上的点，其中n∈N*，设cn＝an－bn，则cn与cn＋1的大小关系为________．
cn＋1<cn
开心快乐假期作业暑假作业西安出版社系列答案
则
（ ） 
B、
C、
D、
表示该学生选修课程的门数，用
表示该学生选修课程门数和没有选修课程门数的乘积。
为偶函数”为事件A,求事件A的概率；
≤1的解集是( )
，＋∞) B．[1，＋∞)
，则“
”是“
”成立的（ ）