题目内容
成都外国语学校开设了甲,乙,丙三门选修课,学生对每门均可选或不选,且选哪门课程互不影响。已知某学生只选修甲的概率为0.08,只选修甲和乙的概率为0.12,至少选修一门的概率为0.88,用 表示该学生选修课程的门数,用
表示该学生选修课程的门数,用 表示该学生选修课程门数和没有选修课程门数的乘积。
表示该学生选修课程门数和没有选修课程门数的乘积。
(1)记“函数 为偶函数”为事件A,求事件A的概率;
为偶函数”为事件A,求事件A的概率;
(2)求 的分布列与数学期望.
的分布列与数学期望.
解:设该生选修甲,乙,丙课程的概率依次为P1,P2,P3,则由题意知
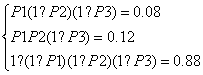 ,解得
,解得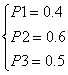 , ………4分
, ………4分
(1)由题意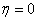 ,即该生为选三门或一门都不选。
,即该生为选三门或一门都不选。
因此P(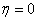 )=0.4´0.6´0.5+(1−0.4)(1−0.6)(1−0.5)=0.24即为所求. ………6分
)=0.4´0.6´0.5+(1−0.4)(1−0.6)(1−0.5)=0.24即为所求. ………6分
(2)由题意可设 可能取的值为0,1,2,3
可能取的值为0,1,2,3
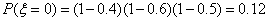 ,
,
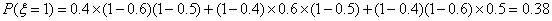
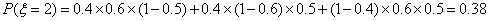
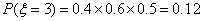
|
| 0 | 1 | 2 | 3 |
| P | 0.12 | 0.38 | 0.38 | 0.12 |
 的分布列为:
的分布列为:
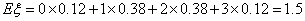 --------------12分
--------------12分

练习册系列答案
相关题目
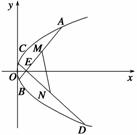
 时,函数
时,函数 始终满足
始终满足 ,则函数
,则函数 的图象大致为( )
的图象大致为( )
 ,其导函数为
,其导函数为 ,则
,则


 +
+ ≥2成立的条件有( )
≥2成立的条件有( )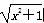 图象上的点,Bn(n,bn)为函数y=x图象上的点,其中n∈N*,设cn=a
图象上的点,Bn(n,bn)为函数y=x图象上的点,其中n∈N*,设cn=a n-bn,则cn与cn+1的大小关系为________.
n-bn,则cn与cn+1的大小关系为________. D.ln 2
D.ln 2 D.|a+b|≥2cd
D.|a+b|≥2cd