题目内容
6.在等比数列{an}中,公比为q,Tn为其前n项之积,则Tn,T2n,T3n有什么样的关系?请给出证明.分析 T3n=($\frac{{T}_{2n}}{{T}_{n}}$)3,利用等比数列的通项公式能进行证明.
解答 解:在等比数列{an}中,公比为q,Tn为其前n项之积,则T3n=($\frac{{T}_{2n}}{{T}_{n}}$)3.
证明如下:
T3n=${a}_{1}×{a}_{1}q×{a}_{1}{q}^{2}×…×{a}_{1}{q}^{3n-1}$=${{a}_{1}}^{3}{q}^{1+2+…+3n-1}$=(${{a}_{1}}^{n}$${q}^{\frac{n(3n-1)}{2}}$)3,
$\frac{{T}_{2n}}{{T}_{n}}$=$\frac{{a}_{1}×{a}_{1}q×{a}_{1}{q}^{2}×…×{a}_{1}{q}^{2n-1}}{{a}_{1}×{a}_{1}q×{a}_{1}{q}^{2}×…×{a}_{1}{q}^{n-1}}$=${{a}_{1}}^{n}$${q}^{\frac{n(3n-1)}{2}}$,
∴T3n=($\frac{{T}_{2n}}{{T}_{n}}$)3.
点评 本题考查等比数列的前n项之积、前2n项之积、前3n项之积的相互关系的判断,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知a>0,x、y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{y≥a(x-3)}\end{array}\right.$ 若z=2x+y的最小值与最大值的和为7,则a=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
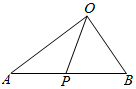 如图,在△AOB中,点P在AB上,且$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$(m∈R),求$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$的值.
如图,在△AOB中,点P在AB上,且$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$(m∈R),求$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$的值.