题目内容
7.若$\overrightarrow{a}$+$\overrightarrow{b}$=(2,-8),$\overrightarrow{a}$-$\overrightarrow{b}$=(-8,16),求$\overrightarrow{a}$•$\overrightarrow{b}$及$\overrightarrow{a}$与$\overrightarrow{b}$夹角θ的余弦值.分析 根据向量的坐标运算法则求出$\overrightarrow{a},\overrightarrow{b}$的坐标,求出数量积和模长,代入夹角公式计算.
解答 解:∵2$\overrightarrow{a}$=($\overrightarrow{a}$+$\overrightarrow{b}$)+($\overrightarrow{a}$-$\overrightarrow{b}$)=(-6,8),∴$\overrightarrow{a}$=(-3,4).
∴$\overrightarrow{b}$=$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{a}$=(5,-12).
∴$\overrightarrow{a}•\overrightarrow{b}$=-15-48=-63.|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=13.
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=-$\frac{63}{65}$.
点评 本题考查了平面向量的坐标运算,数量积运算,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
2.已知α∈(-π,-$\frac{π}{4}$),且sinα=-$\frac{1}{3}$,则cosα等于( )
| A. | -$\frac{2\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $±\frac{2\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
12.已知集合A={y|y=($\frac{1}{2}$)x,x≥-1},B={y|y=ex+1,x≤0},则下列结论正确的是( )
| A. | A=B | B. | A∪B=R | C. | A∩(∁RB)=∅ | D. | B∩(∁RA)=∅ |
19.根据定积分的定义,${∫}_{0}^{2}$x2dx等于( )
| A. | $\sum_{i=1}^{n}$($\frac{i-1}{n}$)2•$\frac{1}{n}$ | B. | $\underset{lim}{n→∞}$$\sum_{i=1}^{n}$($\frac{i-1}{n}$)2•$\frac{1}{n}$ | ||
| C. | $\sum_{i=1}^{n}$($\frac{2i}{n}$)2•$\frac{2}{n}$ | D. | $\underset{lim}{n→∞}$$\sum_{i=1}^{n}$($\frac{2i}{n}$)2•$\frac{2}{n}$ |
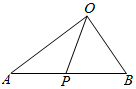 如图,在△AOB中,点P在AB上,且$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$(m∈R),求$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$的值.
如图,在△AOB中,点P在AB上,且$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$(m∈R),求$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$的值.