题目内容
已知命题p:?x∈R,x2-2x+1>0;命题q:?x∈R,sinx=1,则下列判断正确的是( )
| A、p是真命题 |
| B、¬q是假命题 |
| C、¬p是假命题 |
| D、q是假命题 |
考点:复合命题的真假
专题:简易逻辑
分析:命题p:当x=1时,x2-2x+1=0,可知命题p不正确;命题q:当x=2kπ+
(k∈Z)时,sinx=1,可得命题q正确.
| π |
| 2 |
解答:
解:命题p:?x∈R,x2-2x+1=(x-1)2≥0,当x=1时,x2-2x+1=0,因此命题p不正确;
命题q:当x=2kπ+
(k∈Z)时,sinx=1,因此命题q正确.
由以上可知:¬q是假命题.
故选:B.
命题q:当x=2kπ+
| π |
| 2 |
由以上可知:¬q是假命题.
故选:B.
点评:本题考查了简易逻辑的有关知识,属于基础题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
 图1是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到12次的考试成绩依次记为A1,A2,…,A12.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )
图1是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到12次的考试成绩依次记为A1,A2,…,A12.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )| A、8 | B、9 | C、10 | D、11 |
已知向量
=(1,x),
=(1,-x),若2
+
与
垂直,则|
|=( )
| a |
| b |
| a |
| b |
| b |
| a |
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
设集合U={1,2,3,4},A={1,2},B={2,3},则∁U(A∪B)=( )
| A、{1,2,3} | B、{4} |
| C、{2} | D、{1,4} |
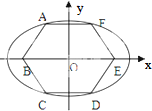 如图正六边形ABCDEF中,B、E为椭圆的焦点,A、C、D、F在椭圆上,则椭圆的离心率为( )
如图正六边形ABCDEF中,B、E为椭圆的焦点,A、C、D、F在椭圆上,则椭圆的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知向量
=(λ,2),
=(1,-2),
⊥
,则实数λ=( )
| a |
| b |
| a |
| b |
| A、1 | B、4 | C、-1 | D、-4 |
掷一枚质地均匀的骰子,则掷得点数为1的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )
| A、假设三内角都不大于60度 |
| B、假设三内角至多有一个大于60度 |
| C、假设三内角都大于60度 |
| D、假设三内角至多有两个大于60度 |