题目内容
13．已知命题p：|x|＞a，q：$\frac{x-1}{2x-1}$＞0．若p是q的必要不充分条件．则实数a的取值范围是a＜0．分析 通过讨论a化简命题p，通过解分式不等式化简命题q，根据集合的包含关系，列出不等式组求出a的范围．
解答 解：若a＜0，则p：x∈R，满足p是q的必要不充分条件，
若a≥0，则由|x|＞a，得x＞a或x＜-a，
即p：x＞a或x＜-a，
q：$\frac{x-1}{2x-1}$＞0，
所以，x＞1或x＜$\frac{1}{2}$；
因为p是q的必要不充分条件，
∴$\left\{\begin{array}{l}{a≤1}\\{-a≥\frac{1}{2}}\end{array}\right.$（“=”不同时取到），解得：a≤-$\frac{1}{2}$，不合题意，
综上，a＜0，
故答案为：a＜0．
点评 判断一个命题是另一个命题的什么条件问题，应该先化简各个命题，然后再进行判断，若命题中是数集，常转化为集合的包含关系问题来解决．
练习册系列答案
相关题目
3．设椭圆的标准方程为$\frac{x^2}{9-k}+\frac{y^2}{5-k}=1$，若焦点在x轴上，则实数k的取值范围是（ ）
| A． | k＞5 | B． | 5＜k＜9 | C． | k＜5 | D． | k＞9 |
4．已知全集U={y|y=x3，x=-1，0，1，2}，集合A={-1，1}，B={1，8}，则A∩（∁UB）=（ ）
| A． | {-1，1} | B． | {-1} | C． | {1} | D． | ∅ |
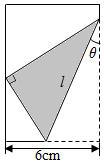如图，将矩形纸片的右下角折起，使得该角的顶点落在矩形的左边上，那么折痕长度l取决于角θ的大小，探求l，θ之间的关系式，并导出用θ表示l的函数表达式．