题目内容
已知tan α=-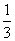 ,cos β=
,cos β=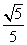 ,α,β∈(0,π).
,α,β∈(0,π).
(1)求tan(α+β)的值;
(2)求函数f(x)=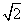 sin(x-α)+cos(x+β)的最大值.
sin(x-α)+cos(x+β)的最大值.
解 (1)由cos β=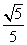 ,β∈(0,π),
,β∈(0,π),
得sin β=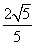 ,tan β=2,
,tan β=2,
所以tan(α+β)=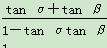 =1.
=1.
(2)因为tan α=-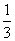 ,α∈(0,π),
,α∈(0,π),
所以sin α=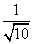 ,cos α=-
,cos α=-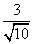 ,
,
f(x)=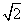 (sin xcos α-cos xsin α)+cos xcos β-sin xsin β
(sin xcos α-cos xsin α)+cos xcos β-sin xsin β
=-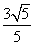 sin x-
sin x-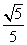 cos x+
cos x+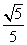 cos x-
cos x-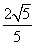 sin x
sin x
=-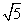 sin x,
sin x,
又-1≤sin x≤1,所以f(x)的最大值为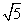 .
.

练习册系列答案
相关题目
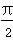 )的图象与y轴交于点(0,
)的图象与y轴交于点(0, ),且该函数的最小正周期为π.
),且该函数的最小正周期为π.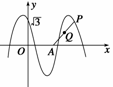
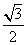 ,x0∈[
,x0∈[ ,则2x与πsin x的大小关系是( )
,则2x与πsin x的大小关系是( )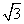 sin A,sin B),n=(cos B,
sin A,sin B),n=(cos B,
 的图象的一条对称轴方程是( )
的图象的一条对称轴方程是( )
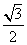 ,则有( )
,则有( )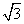 cos x(x∈[-π,0])的单调递增区间是( )
cos x(x∈[-π,0])的单调递增区间是( )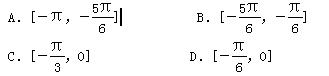
 则目标函数z=|x+3y|的最大值为( )
则目标函数z=|x+3y|的最大值为( )