题目内容
设m,n是两条不同的直线,α,β是两个不同的平面,则下列说法正确的是( )
| A、若m⊥n,m⊥α,则n∥α |
| B、若m∥α,α⊥β,则m⊥β |
| C、若m⊥β,α⊥β,则m∥α |
| D、若m⊥n,m⊥α,n⊥β,则α⊥β |
考点:空间中直线与平面之间的位置关系,空间中直线与直线之间的位置关系,平面与平面之间的位置关系
专题:空间位置关系与距离
分析:利用线面平行、线面垂直以及面面垂直的性质定理和判定定理对四个选项分别分析选择.
解答:
解:对于A,若m⊥n,m⊥α,则n可能在α内;故A错误;
对于B,若m∥α,α⊥β,则m与β相交或者在β或者平行于β,故B错误;
对于C,若m⊥β,α⊥β,则m∥α或者m?α;故C错误;
对于D,若m⊥n,m⊥α,n⊥β,根据线面垂直的性质定理和判定定理可以判断α⊥β;故D正确;
故选D.
对于B,若m∥α,α⊥β,则m与β相交或者在β或者平行于β,故B错误;
对于C,若m⊥β,α⊥β,则m∥α或者m?α;故C错误;
对于D,若m⊥n,m⊥α,n⊥β,根据线面垂直的性质定理和判定定理可以判断α⊥β;故D正确;
故选D.
点评:本题考查了线面平行、线面垂直以及面面垂直的性质定理和判定定理;关键是熟练掌握性质定理和判定定理,正确运用.

练习册系列答案
相关题目
已知等差数列 {an}的公差为2,若a1,a3,a4成等比数列,则a2等于( )
| A、.-6 | B、-4 |
| C、-8 | D、-10 |
执行如图所示的程序框图,则输出的S为( )


| A、3 | B、7 | C、10 | D、16 |
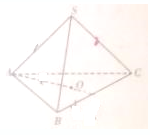 如图,在三棱锥S-ABC中,AB=AC,顶点S在底面ABC上的射影是△ABC的重心O,BC=8,AO=2,SA=
如图,在三棱锥S-ABC中,AB=AC,顶点S在底面ABC上的射影是△ABC的重心O,BC=8,AO=2,SA=