题目内容
20.若角α的顶点与平面直角坐标系的原点重合,始边与x轴的非负半轴重合,终边以原点为圆心的单位圆交于点(m,n),且$\frac{n}{m}=-2$,则2sinαcosα-cos2α等于( )| A. | -2 | B. | -1 | C. | $-\frac{1}{2}$ | D. | 2 |
分析 由已知及三角函数定义求出tanα的值小于0,再由α的范围,确定出sinα和cosα的值,然后代入计算即可得答案.
解答 解:由已知条件及三角函数定义,得到tanα=$\frac{n}{m}=-2$,又α∈[0,π),
∴sinα=$\frac{2\sqrt{5}}{5}$,cosα=-$\frac{\sqrt{5}}{5}$.
∴2sinαcosα-cos2α=$2×\frac{2\sqrt{5}}{5}×(-\frac{\sqrt{5}}{5})-(-\frac{\sqrt{5}}{5})^{2}$=$-\frac{4}{5}-\frac{1}{5}=-1$.
故选:B.
点评 本题考查了三角函数的化简求值,考查了任意角的三角函数定义,是基础题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
12.已知向量$\overrightarrow{AB}=(2,-1)$,$\overrightarrow{AC}=(-4,1)$,向量$\overrightarrow{BC}$的坐标是( )
| A. | (-6,2) | B. | (6,-2) | C. | (-2,0) | D. | (2,0) |
8.已知向量$\overrightarrow{AB}=(2,-1)$,$\overrightarrow{BC}=(-4,1)$,向量$\overrightarrow{AC}$的坐标是( )
| A. | (-6,2) | B. | (6,-2) | C. | (-2,0) | D. | (2,0) |
5.函数f(x)=(2x-1)ex的递增区间为( )
| A. | (-∞,+∞) | B. | $({\frac{1}{2},+∞})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-\frac{1}{2},+∞})$ |
8.已知命题p1:?x0∈R,x02+x0+1<0;p2:?x∈[1,2],x2-1≥0.以下命题为真命题的是( )
| A. | (¬p1)∧(¬p2) | B. | p1∨(¬p2) | C. | (¬p1)∧p2 | D. | p1∧p2 |
9.根据如图的流程图,可得的结果是( )
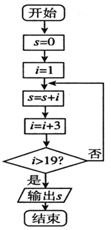

| A. | 76 | B. | 70 | C. | 51 | D. | 19 |
