题目内容
8．已知z1=1-i，z2=2+2i．（1）求z1•z2；
（2）若$\frac{1}{z}$=$\frac{1}{{z}_{1}}$+$\frac{1}{{z}_{2}}$，求z．
分析 （1）直接利用复数代数形式的乘法运算化简得答案；
（2）把已知等式通分变形求得z，代入z1、z2，再由复数代数形式的乘除运算化简得答案．
解答 解：（1）∵z1=1-i，z2=2+2i．
∴z1•z2=（1-i）（2+2i）=4；
（2）由$\frac{1}{z}$=$\frac{1}{{z}_{1}}$+$\frac{1}{{z}_{2}}$，得$z=\frac{{z}_{1}•{z}_{2}}{{z}_{1}+{z}_{2}}=\frac{4}{（1-i）+（2+2i）}=\frac{4}{3+i}=\frac{6}{5}-\frac{2}{5}i$．
点评 本题考查复数代数形式的乘除运算，是基础题．
练习册系列答案
相关题目
16．
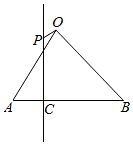如图，在等腰直角△ABO中，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，C为AB上靠近A点的三等分点，过C作AB的垂线l，设P为垂线上任一点，$\overrightarrow{OP}$=$\overrightarrow{p}$，则$\overrightarrow{p}$•（$\overrightarrow{b}$-$\overrightarrow{a}$）=（ ）
如图，在等腰直角△ABO中，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，C为AB上靠近A点的三等分点，过C作AB的垂线l，设P为垂线上任一点，$\overrightarrow{OP}$=$\overrightarrow{p}$，则$\overrightarrow{p}$•（$\overrightarrow{b}$-$\overrightarrow{a}$）=（ ）| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | -$\frac{3}{2}$ | D． | $\frac{3}{2}$ |
13．
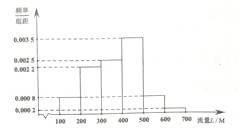某学校为鼓励家校互动，与某手机通讯商合作，为教师伴侣流量套餐，为了解该校教师手机流量使用情况，通过抽样，得到100位教师近2年每人手机月平均使用流量L（单位：M）的数据，其频率分布直方图如下：若将每位教师的手机月平均使用流量分布视为其手机月使用流量，并将频率为概率，回答以下问题．
（1）从该校教师中随机抽取3人，求这3人中至多有1人月使用流量不超过300M的概率；
（2）现该通讯商推出三款流量套餐，详情如下：
这三款套餐都有如下附加条款：套餐费月初一次性收取，手机使用一旦超出套餐流量，系统就自动帮用户充值200M流量，资费20元；如果又超出充值流量，系统就再次自动帮用户充值200M流量，资费20元/次，依此类推，如果当流量有剩余，系统将自动清零，无法转入次月使用．
学校欲订购其中一款流量套餐，为教师支付月套餐费，并承担系统自动充值的流量资费的75%，其余部分由教师个人承担，问学校订购哪一款套餐最经济？说明理由．
某学校为鼓励家校互动，与某手机通讯商合作，为教师伴侣流量套餐，为了解该校教师手机流量使用情况，通过抽样，得到100位教师近2年每人手机月平均使用流量L（单位：M）的数据，其频率分布直方图如下：若将每位教师的手机月平均使用流量分布视为其手机月使用流量，并将频率为概率，回答以下问题．（1）从该校教师中随机抽取3人，求这3人中至多有1人月使用流量不超过300M的概率；
（2）现该通讯商推出三款流量套餐，详情如下：
| 套餐名称 | 月套餐费（单位：元） | 月套餐流量（单位：M） |
| A | 20 | 300 |
| B | 30 | 500 |
| C | 38 | 700 |
学校欲订购其中一款流量套餐，为教师支付月套餐费，并承担系统自动充值的流量资费的75%，其余部分由教师个人承担，问学校订购哪一款套餐最经济？说明理由．