题目内容
9.若函数$f(x)=\left\{\begin{array}{l}{log_a}x,x>2\\-{x^2}+2x-2,x≤2\end{array}\right.$(a>0,a≠1)的值域是(-∞,-1],则实数a的取值范围是[$\frac{1}{2}$,1).分析 根据二次函数的性质求出f(x)在(-∞,2]的最大值,从而判断出a的范围即可.
解答 解:x≤2时:f(x)=-x2+2x-2=-(x-1)2-1,
对称轴x=1,f(x)在(-∞,1)递增,在(1,2]递减;
∴f(x)的最大值是-1,而f(x)的值域是(-∞,-1],
故0<a<1,
∴${log}_{a}^{2}$≤-1,解得:a≥$\frac{1}{2}$,
故答案为:[$\frac{1}{2}$,1).
点评 本题考查了分段函数问题,考查二次函数以及对数函数的性质,是一道基础题.

练习册系列答案
相关题目
20.已知集合A={x|$\frac{x-2}{x}$≤0},B={x|-2≤x≤1},则A∩B=( )
| A. | [0,1] | B. | (0,1) | C. | [0,1) | D. | (0,1] |
4.已知F1(-3,0),F2(3,0),动点M满足|MF1|+|MF2|=5,则点M的轨迹是( )
| A. | 双曲线 | B. | 椭圆 | C. | 线段 | D. | 不存在 |
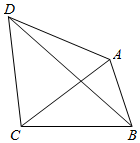 如图所示在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD的面积的最大值为$\sqrt{3}$+1.
如图所示在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD的面积的最大值为$\sqrt{3}$+1.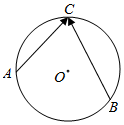 如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4].
如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4].