题目内容
如图，正三角形ABC外接圆的半径为1，点M、N分别是边AB、AC的中点，延长MN与△ABC的外接圆交于点P，求线段NP的长．
解：设正三角形ABC的边长为x，由正弦定理，得
＝2，所以x＝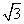
.延长PN交圆于Q，则NA·NC＝NP·NQ.设NP＝t，则
＝
.所以t＝
，即NP＝.
练习册系列答案
相关题目
题目内容
如图，正三角形ABC外接圆的半径为1，点M、N分别是边AB、AC的中点，延长MN与△ABC的外接圆交于点P，求线段NP的长．
解：设正三角形ABC的边长为x，由正弦定理，得＝2，所以x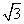＝.延长PN交圆于Q，则NA·NC＝NP·NQ.设NP＝t，则＝.所以t＝，即NP＝.
化为普通方程，并说明它表示的图形．
＝3，n∈N*，若数列{cn}满足cn＝ban，则c2 013＝( )
＜0.如果f
＝
，4f(log
x)＞3，那么x的取值范围为( )
B. 
D.
∪