题目内容
已知关于x的不等式|ax-1|+|ax-a|≥2(a>0).
(1) 当a=1时,求此不等式的解集;
(2) 若此不等式的解集为R,求实数a的取值范围.
解:(1) 当a=1时,不等式为|x-1|≥1,∴ x≥2或x≤0,
∴ 不等式解集为{x|x≤0或x≥2}.
(2) 不等式的解集为R,即|ax-1|+|ax-a|≥2(a>0)恒成立.
∵ |ax-1|+|ax-a|=
∴ a =|a-1|≥2.∵ a>0,∴ a≥3,
=|a-1|≥2.∵ a>0,∴ a≥3,
∴ 实数a的取值范围为[3,+∞).

练习册系列答案
相关题目
 (t为参数),C2:
(t为参数),C2: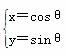 (θ为参数).
(θ为参数).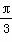 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
 +1.
+1. .
.
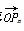 ·OPn+1的最小值;
·OPn+1的最小值;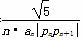 (n≥2),求c2+c3+c4+…+cn的值.
(n≥2),求c2+c3+c4+…+cn的值. 上只有一个零点,求实数a的取值范围.
上只有一个零点,求实数a的取值范围.