题目内容
3.定义在(0,+∞)上的函数f(x)满足f(x)>2(x+$\sqrt{x}$)f′(x),其中f′(x)为f(x)的导函数,则下列不等式中,一定成立的是( )| A. | f(1)>$\frac{f(2)}{2}$>$\frac{f(3)}{3}$ | B. | $\frac{f(1)}{2}$>$\frac{f(4)}{3}$>$\frac{f(9)}{4}$ | C. | f(1)<$\frac{f(2)}{2}$<$\frac{f(3)}{3}$ | D. | $\frac{f(1)}{2}$<$\frac{f(4)}{3}$<$\frac{f(9)}{4}$ |
分析 由题意构造函数g(x)=$\frac{f(x)}{\sqrt{x}+1}$,再由导函数的符号判断出函数g(x)的单调性,由函数g(x)的单调性即可得出正确选项.
解答 解:构造函数g(x)=$\frac{f(x)}{\sqrt{x}+1}$,
则g′(x)=$\frac{f′(x)•(\sqrt{x}+1)-f(x)•\frac{1}{2\sqrt{x}}}{(\sqrt{x}+1)^{2}}$=$\frac{2(x+\sqrt{x})f′(x)-f(x)}{2\sqrt{2}x•(\sqrt{x}+1)^{2}}$,
∵在(0,+∞)上的函数f(x)满足f(x)>2(x+$\sqrt{x}$)f′(x),
∴g′(x)<0,
∴g(x)=$\frac{f(x)}{\sqrt{x}+1}$在(0,+∞)上单调递减,
∴g(1)>g(4)>g(9),
∴$\frac{f(1)}{1+1}$>$\frac{f(4)}{2+1}$>$\frac{f(9)}{3+1}$,
∴$\frac{f(1)}{2}$>$\frac{f(4)}{3}$>$\frac{f(9)}{4}$,
故选:B
点评 本题考查了由条件构造函数和用导函数的符号判断函数的单调性,利用函数的单调性的关系对不等式进行判断.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
13.2017年4月14日,某财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象.为了研究使用淡化海砂与混凝土耐久性是否达标有关,某大学实验室随机抽取了60个样本,得到了相关数据如表:
(Ⅰ)根据表中数据,求出s,t的值;
(Ⅱ)利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下认为使用淡化海砂与混凝土耐久性是否达标有关?
参考数据:
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| 混凝土耐久性达标 | 混凝土耐久性不达标 | 总计 | |
| 使用淡化海砂 | 25 | t | 30 |
| 使用未经淡化海砂 | s | ||
| 总计 | 40 | 60 |
(Ⅱ)利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下认为使用淡化海砂与混凝土耐久性是否达标有关?
参考数据:
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
14.设实数a,b,c,d,e同时满足关系:a+b+c+d+e=8,a2+b2+c2+d2+e2=16,则实数e的最大值为( )
| A. | 2 | B. | $\frac{16}{5}$ | C. | 3 | D. | $\frac{2}{5}$ |
11.某程序框图如图所示,若输入的t=4,则输出的k等于( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
8.在数列{an}中,若$\sqrt{{a}_{n+1}}$=$\sqrt{{a}_{n}}$+$\sqrt{2}$,a1=8,则数列{an}的通项公式为( )
| A. | an=2(n+1)2 | B. | an=4(n+1) | C. | an=8n2 | D. | an=4n(n+1) |
12.已知集合$A=\{x|{log_{\frac{1}{3}}}(4-x)>-1\}$,B={x|4x-1>8},若全集为实数集R,则A∩(∁RB)=( )
| A. | $(-∞,\frac{5}{2}]$ | B. | (2,4) | C. | $(\frac{5}{2},4)$ | D. | (1,$\frac{5}{2}$] |
1.设函数f(x)与函数g(x)是定义在同一区间上的两个函数,若函数y=f(x)-g(x)在次区间上有两个不同的零点,则称函数f(x),g(x)在此区间上是“交织函数”,若f(x)=4|x|-$\frac{9}{4}$与g(x)=2x+m在(-∞,+∞)上是“交织函数”,则m的取值范围为( )
| A. | (-$\frac{9}{4}$,-2] | B. | [-1,0] | C. | (-∞,-2] | D. | (-$\frac{9}{4}$,+∞) |
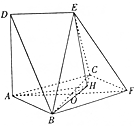 如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF,且∠DAF=90°.
如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF,且∠DAF=90°.