题目内容
已知数列{an}的通项公式为an=lg(1+
),n=1,2,3,…,Sn是数列{an}的前n项和,则Sn=( )
| 2 |
| n2+3n |
| A、0 | ||
B、lg
| ||
C、lg
| ||
D、lg
|
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:an=lg(1+
)=lg
=lg
-lg
,利用裂项相消法即可求得Sn.
| 2 |
| n2+3n |
| (n+1)(n+2) |
| n(n+3) |
| n+1 |
| n |
| n+3 |
| n+2 |
解答:
解:∵an=lg(1+
)=lg
=lg
-lg
,
∴Sn=lg2-lg
+lg
-lg
+lg
-lg
+…+lg
-lg
+lg
-lg
=lg2+lg
-lg
-lg
=lg3+lg
,
故选:B.
| 2 |
| n2+3n |
| (n+1)(n+2) |
| n(n+3) |
| n+1 |
| n |
| n+3 |
| n+2 |
∴Sn=lg2-lg
| 4 |
| 3 |
| 3 |
| 2 |
| 5 |
| 4 |
| 4 |
| 3 |
| 5 |
| 4 |
| n |
| n-1 |
| n+2 |
| n+1 |
| n+1 |
| n |
| n+3 |
| n+2 |
=lg2+lg
| 3 |
| 2 |
| n+2 |
| n+1 |
| n+3 |
| n+2 |
=lg3+lg
| n+1 |
| n+3 |
故选:B.
点评:该题考查数列求和,属中档题,熟练裂项求和法是解题基础,合理对通项进行拆项是解题关键,注意观察消项规律.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
一个容量为20的数据样本,分组与频数为:[10,20]2个,(20,30]3个,(30,40]4个,(40,50]5个,(50,60]4个,(60,70]2个,则样本数据在区间(-∞,50)上的可能性为( )
| A、5% | B、25% |
| C、50% | D、70% |
函数f(x)=
的定义域为( )
| 1 |
| ln(x+1) |
| A、(-1,0)∪(0,+∞) |
| B、[-1,0)∪(0,+∞) |
| C、[-1,+∞) |
| D、(-1,+∞) |
M={x∈R|x≥2},a=π,则下列四个式子①a∈M;②{a}?M; ③a⊆M;④{a}∩M=π,其中正确的是( )
| A、①② | B、①④ | C、②③ | D、①②④ |
已知实数x>y,且y≠0,则下列结论正确的是( )
A、
| ||||
| B、cx>cy(c∈R) | ||||
| C、x3>y3 | ||||
D、
|
已知三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,且PA=1,则点A到平面PBC的距离为( )
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
在等差数列{an}中,已知a1=
,a4+a5=
,若an=33,则n=( )
| 1 |
| 3 |
| 16 |
| 3 |
| A、50 | B、49 | C、48 | D、47 |
数列{an}前六项是1,2,4,8,16,它的一个通项公式是( )
| A、an=2n |
| B、an=2n |
| C、an=2n+1 |
| D、an=2n-1 |
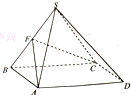 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠DAB=135°,BC=2