题目内容
14.已知函数f(x)=x2-2ax+5,(a∈R).(1)求函数f(x)在[-2,2]上的最小值g(a)的表达式
(2)若函数f(x)在区间(-∞,2]上是单调递减的,且对于任意的x1、x2∈[1,a+1],总有|f(x1)-
f(x2)|≤4,求实数a的取值范围.
分析 (1)分对称轴和闭区间的三种位置关系:轴在区间左边,轴在区间右边,轴在区间中间来讨论即可;
(2)由条件利用二次函数的性质可得a≥2.故只要f(1)-f(a)≤4即可,即(a-1)2≤4,求得a的范围.
解答 解:(1)∵f(x)=x2-2ax+5=(x-a)2+5-a2,对称轴是x=a,
当a<-2时,f(x)=x2-2ax+5在[-2,2]上是增函数,
故最小值g(a)=f(-2)=9+4a;
当a>2时,f(x)=x2-2ax+5在[-2,2]上是减函数,
故最小值g(a)=f(2)=9-4a;
当-2≤a≤2时,f(x)=x2-2ax+5在[-2,2]的最小值g(a)=f(a)=5-a2,
综上得,二次函数f(x)=x2-2ax+5在[-2,2]上的最小值
g(a)=$\left\{\begin{array}{l}{9+4a,a<-2}\\{5-{a}^{2},-2≤a≤2}\\{9-4a,a>2}\end{array}\right.$.
(2)由于函数f(x)=x2-2ax+5的图象的对称轴为x=a,
函数f(x)=x2-2ax+5在区间(-∞,2]上单调递减,即有a≥2.
故在区间∈[1,a+1]上,1离对称轴x=a最远,
故要使对任意的x1,x2∈[1,a+1],都有|f(x1)-f(x2)|≤4,
只要f(1)-f(a)≤4即可,即(a-1)2≤4,求得-1≤a≤3.
再结合 a≥2,可得2≤a≤3,
则a的取值范围是[2,3].
点评 本题的实质是求二次函数的最值问题,关于解析式中带参数的二次函数在固定闭区间上的最值问题,一般是根据对称轴和闭区间的位置,同时考查绝对值不等式的解法,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
4.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的两个焦点,若双曲线上存在一点P,使得|PF1|,2a,|PF2|成等差数列,则双曲线离心率的取值范围是( )
| A. | (1,2) | B. | (1,2] | C. | [2,+∞) | D. | (2,+∞) |
5.红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量
m(件)与时间t(天)的关系如表所示.
未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1=$\frac{1}{4}$t+25(1≤t≤20,且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系为y2=$\frac{1}{2}$t+40(21≤t≤40,且t为整数).下面我们就来研究销售这种商品的有关问题.
(1)认真分析表格中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些 数据的m(件)与t(天)的关系式.
(2)试预测未来40天中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的前20天中,该公司决定每销售1件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
m(件)与时间t(天)的关系如表所示.
| 时间t/天 | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量 m/件 | 94 | 90 | 84 | 76 | 24 | … |
(1)认真分析表格中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些 数据的m(件)与t(天)的关系式.
(2)试预测未来40天中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的前20天中,该公司决定每销售1件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
2.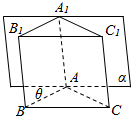 已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )
已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )
 已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )
已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )| A. | $\sqrt{3}$ | B. | 4 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
9.随机变量X的分布列如表所示,则EX=1.7.
| X | 0 | 1 | 2 | 3 |
| p | 0.1 | 0.3 | 0.4 | 0.2 |
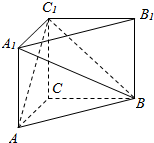 如图:在直三棱柱ABC-A1B1C1中,AA1=BC=AC=2,AC⊥BC.
如图:在直三棱柱ABC-A1B1C1中,AA1=BC=AC=2,AC⊥BC.