题目内容
2.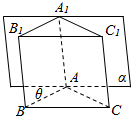 已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )
已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的值不可能是( )| A. | $\sqrt{3}$ | B. | 4 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
分析 根据已知条件,求出AB与投影面α所成角为为θ时,mn的取值范围,进而分析四个答案哪一个不在该范围内,可得答案.
解答 解:AB与投影面α所成角为为θ时,平面ABC如下图所示: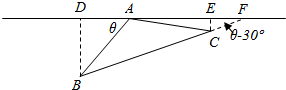
∵∠BAC=120°,AB=AC=1,AA1=2,∠BAD=θ,
∴BC=$\sqrt{3}$,∠BFD=θ-30°,
∴BD=sinθ,DE=$\sqrt{3}$cos(θ-30°),
故m=2$\sqrt{3}$cos(θ-30°),n=$\sqrt{3}$sinθ,
∴mn=6sinθ($\frac{\sqrt{3}}{2}$cosθ+$\frac{1}{2}$sinθ)=3$\sqrt{3}$sinθcosθ+3sin2θ=$\frac{3\sqrt{3}}{2}$sin2θ+$\frac{3}{2}$(1-cos2θ)=$\frac{3\sqrt{3}}{2}$sin2θ-$\frac{3}{2}$cos2θ+$\frac{3}{2}$=3sin(2θ-30°)+$\frac{3}{2}$,
∵30°≤θ≤60°
∴30°≤2θ-30°≤90°,
故3≤3sin(2θ-30°)+$\frac{3}{2}$≤$\frac{9}{2}$,
∵$\sqrt{3}$∈[3,$\frac{9}{2}$],
故mn的值不可能是$\sqrt{3}$,
故选:A.
点评 本题考查的知识点是三视图,三角恒等变换,正弦型函数的图象和性质,是三角函数与立体几何的综合应用,难度中档.

练习册系列答案
相关题目
13.一艘船以20km/h的速度向正北航行,船在A处看见灯塔B在船的东北方向,1h后船在C处看见灯塔B在船的北偏东75°的方向上,这时船与灯塔的距离BC等于( )
| A. | 20$\sqrt{2}$ | B. | 20 | C. | 20$\sqrt{3}$ | D. | 10$\sqrt{2}$ |
10.如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的表面积为( )
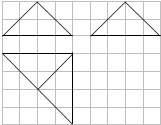

| A. | 8+12$\sqrt{2}$ | B. | 16+24$\sqrt{2}$ | C. | $\frac{1}{3}(8+12\sqrt{2})$ | D. | 4+6$\sqrt{2}$ |
17.如图是一个空间几何体的三视图,则该几体体的外接球的体积是( )
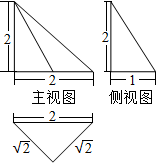

| A. | $\frac{64\sqrt{2}}{3}$π | B. | $\frac{32\sqrt{2}}{3}$π | C. | $\frac{8\sqrt{2}}{3}$π | D. | 8π |
7.某几何体的正(主)视图和侧(左)视图如图所示,则该几何体的体积不可能是( )
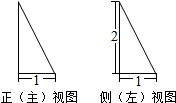

| A. | $\frac{1}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2}{3}$ | D. | 1 |
12.平行六面体ABCD-A1B1C1D1中,AB=5,AD=3,AA1=7,∠CBA=120°,∠BAA1=∠DAA1=45°,则AC1的长等于( )
| A. | 83 | B. | $\sqrt{83}$ | C. | 98$+56\sqrt{2}$ | D. | $\sqrt{98+56\sqrt{2}}$ |
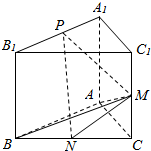 如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.
如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.