题目内容
11.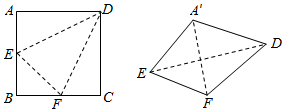 如图,边长为2的正方形ABCD中,点E、F分别是AB、BC的中点,将△ADE、△EBF、△FCD分别沿DE、EF、FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为$\frac{\sqrt{6}}{2}$.
如图,边长为2的正方形ABCD中,点E、F分别是AB、BC的中点,将△ADE、△EBF、△FCD分别沿DE、EF、FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为$\frac{\sqrt{6}}{2}$.
分析 把棱锥扩展为正四棱柱,求出正四棱柱的外接球的半径就是三棱锥的外接球的半径.
解答 解:由题意可知△A′EF是等腰直角三角形,且A′D⊥平面A′EF.
三棱锥的底面A′EF扩展为边长为1的正方形,
然后扩展为正四棱柱,三棱锥的外接球与正四棱柱的外接球是同一个球,
正四棱柱的对角线的长度就是外接球的直径,直径为:$\sqrt{{1}^{2}+{1}^{2}+{2}^{2}}$=$\sqrt{6}$.
∴球的半径为$\frac{\sqrt{6}}{2}$.
故答案为:$\frac{\sqrt{6}}{2}$.
点评 本题考查三棱锥的外接球体积,考查学生的计算能力,确定三棱锥的外接球的半径是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.某单位有老年人28人,中年人56人,青年人84人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36的样本,则老年人、中年人、青年人分别抽取的人数是( )
| A. | 6,12,18 | B. | 7,11,19 | C. | 6,13,17 | D. | 7,12,17 |
6.已知函数$f(g(x))=sin2x,g(x)=tan({x+\frac{π}{4}})$,则$f(-\frac{1}{7})$=( )
| A. | $\frac{4}{3}$ | B. | $-\frac{4}{3}$ | C. | $-\frac{24}{25}$ | D. | $-\frac{24}{7}$ |
16.已知等比数列{an}的公比为4,且a1+a2=20,设bn=log2an,则b2+b4+b6+…+b2n等于( )
| A. | n2+n | B. | 2n2+n | C. | 2(n2+n) | D. | 4(n2+n) |
20.从5名学生中选2名学生参加周日社会实验活动,学生甲被选中而学生乙没有被选中的方法种数是( )
| A. | 10 | B. | 6 | C. | 4 | D. | 3 |
1.若一球的半径为r.则内接于球的圆柱的最大侧面积为( )
| A. | 2πr2 | B. | πr2 | C. | 4πr2 | D. | $\frac{1}{2}$πr2 |