题目内容

16．已知等比数列{an}的公比为4，且a1+a2=20，设bn=log2an，则b2+b4+b6+…+b2n等于（　　）
A．n2+nB．2n2+nC．2（n2+n）D．4（n2+n）

分析 利用等比数列的通项公式及其前n项和公式即可得出．

解答 解：等比数列{an}的公比为4，且a1+a2=20，
∴a1（1+4）=20，解得a1=4．
∴an=4n．
设bn=log2an=2n，
∴b2n=4n．
则b2+b4+b6+…+b2n=$\frac{n（4+4n）}{2}$=2n2+2n．
故选：C．

点评 本题考查了等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
6．某单位为了了解用电量Y（度）与气温x（℃）之间的关系，随机统计了某4天的用电量与当天气温数据如表格所示．若由表中数据得回归直线方程y=bx+a中b=-2，据此预测当气温为15℃时，用电量的度数约为（　　）
气温（℃）141286
用电量（度）22263438
A．20B．25C．30D．35
7．已知$\overrightarrow{a}$=（-1，1，2），$\overrightarrow{b}$=（2，1，1）则（2$\overrightarrow{a}$+$\overrightarrow{b}$）•$\overrightarrow{b}$=8．
4．已知点P在正△ABC所确定的平面上，且满足$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{AB}$，则△ABP的面积与△BCP的面积之比为（　　）
A．1：1B．1：2C．1：3D．1：4
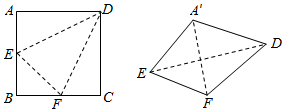11．如图，边长为2的正方形ABCD中，点E、F分别是AB、BC的中点，将△ADE、△EBF、△FCD分别沿DE、EF、FD折起，使得A、B、C三点重合于点A′，若四面体A′EFD的四个顶点在同一个球面上，则该球的半径为$\frac{\sqrt{6}}{2}$．
1．已知函数f（x）=x2+2x，$g（x）={（\frac{1}{2}）^x}+m$，若任意x1∈[1，2]，存在x2∈[-1，1]，使得f（x1）≥g（x2），则实数m的取值范围是m≤$\frac{5}{2}$．
8．货车欲以x km/h的速度行驶去130km远的某地，按交通法规，限制x的允许范围是[50，100]，假设汽油的价格为2元/升，而汽车耗油的速率是（2+$\frac{{x}^{2}}{360}$） 升/小时．司机的工资是14元/小时，试问最经济的车速是18$\sqrt{10}$km/h．这次行车的总费用最低是26$\sqrt{10}$元．
5．函数$f（x）={log_{\frac{1}{2}}}（{{x^2}-2x-3}）+\sqrt{x-1}$的定义域为（3，+∞）．
6．如图，三棱锥P-ABC中，△PAB为边长等于2的正三角形，侧面PAB与底面ABC垂直，∠ABC=90°．
（1）求证：BC⊥PA；
（2）若侧棱PC在底面ABC上投影长为$\sqrt{3}$，求三棱锥P-ABC的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网