题目内容
(本小题满分14分)已知函数 (
( 是常数).
是常数).
(1)设 ,
, 、
、 是函数
是函数 的极值点,试证明曲线
的极值点,试证明曲线 关于点
关于点 对称;
对称;
(2)是否存在常数 ,使得
,使得 ,
, 恒成立?若存在,求常数
恒成立?若存在,求常数 的值或取值范围;若不存在,请说明理由.
的值或取值范围;若不存在,请说明理由.
(注:,对于曲线 上任意一点
上任意一点 ,若点
,若点 关于
关于 的对称点为
的对称点为 ,则
,则 在曲线
在曲线 上.)
上.)
【解析】
试题分析:(1)首先由题意求得 ,由中点坐标公式得到曲线
,由中点坐标公式得到曲线 上任意一点
上任意一点 关于
关于 对称的点为
对称的点为 ,经过计算
,经过计算 ,点
,点 在曲线
在曲线 上,所以,曲线
上,所以,曲线 关于点
关于点 对称
对称
(2)由题 即
即 ,
, ,
, 时,不等式恒成立;
时,不等式恒成立;
 时,不等式等价于
时,不等式等价于 ,构造函数
,构造函数 ,
,
求导讨论 ,
, 在
在 的单调性,进而求出在
的单调性,进而求出在 上这两个函数的最值,即为
上这两个函数的最值,即为 的取值范围。
的取值范围。
试题解析:(1) ,
,
解 得
得 ,
, ,
,
 即
即
曲线 上任意一点
上任意一点 关于
关于 对称的点为
对称的点为
直接计算知, ,点
,点 在曲线
在曲线 上,所以,曲线
上,所以,曲线 关于点
关于点 对称
对称
(2) 即
即 ,
,
 时,不等式恒成立;
时,不等式恒成立;
 时,不等式等价于
时,不等式等价于
作 ,
, ,
, ,
, ,解
,解 、
、 得
得 、
、
|
|
|
|
|
| - | + | 0 | - |
| ↘ | ↗ | 极大值 | ↘ |
| + | - | - | - |
| ↗ | ↘ | ↘ |
 ,
, ,
, 在
在 的最大值为
的最大值为 ;
; ,
, ,
, 在
在 的最小值为
的最小值为
综上所述, 的取值范围为
的取值范围为
考点:曲线 关于点对称问题,利用导数研究函数的性质;
关于点对称问题,利用导数研究函数的性质;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目









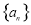 中,
中,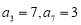 ,则通项公式为
,则通项公式为 ________________.
________________.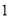 ,侧面积是底面积的
,侧面积是底面积的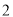 倍,则该圆锥的体积为 .
倍,则该圆锥的体积为 . ,
, 满足约束条件
满足约束条件 ,则
,则 的最小值为 .
的最小值为 .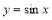 上所有的点横坐标伸长到原来的2倍,纵坐标不变,所得曲线对应的函数的最小正周期
上所有的点横坐标伸长到原来的2倍,纵坐标不变,所得曲线对应的函数的最小正周期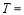
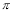 B.
B.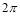 C.
C.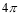 D.
D.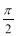
 ,
, .
. 的最小正周期
的最小正周期 和最大值
和最大值 ;
; ,求
,求 的值.
的值. 的离心率
的离心率 .
. 和集合
和集合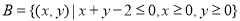 表示的平
表示的平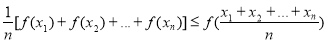 ”,若函数y=sinx 在区间(0,
”,若函数y=sinx 在区间(0,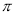 )上是凸函数,则在
)上是凸函数,则在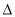 ABC中,sinA+sinB+sinC的最大值是 .
ABC中,sinA+sinB+sinC的最大值是 .