题目内容
已知2cosθ-
=-
,θ∈(
,π),则tanθ= .
| 1-sin2(π-θ) |
| 3 |
| 5 |
| π |
| 2 |
考点:同角三角函数基本关系的运用,运用诱导公式化简求值
专题:三角函数的求值
分析:已知等式左边第二项利用诱导公式及同角三角函数间基本关系化简,再利用二次根式的性质变形求出cosθ的值,进而求出sinθ的值,即可确定出tanθ的值.
解答:
解:∵θ∈(
,π),∴cosθ<0,
已知等式变形得:2cosθ+cosθ=-
,即cosθ=-
,
∴sinθ=
=-
,
则tanθ=-2
.
故答案为:-2
| π |
| 2 |
已知等式变形得:2cosθ+cosθ=-
| 3 |
| 5 |
| 1 |
| 5 |
∴sinθ=
| 1-cos2θ |
2
| ||
| 5 |
则tanθ=-2
| 6 |
故答案为:-2
| 6 |
点评:此题考查了同角三角函数间基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
在下列幂函数中,是偶函数且在(0,+∞)上是增函数的是( )
| A、y=x-2 | ||
B、y=x
| ||
C、y=x
| ||
D、y=x
|
已知sinα=2cosα,则
的值为( )
| sinα+cosα |
| sinα-cosα |
| A、3 | B、-3 | C、2 | D、-2 |
设i为虚数单位,复数 z1=3-ai,z2=1+2i,若
是纯虚数,则实数a的值为( )
| z1 |
| z2 |
A、-
| ||
B、
| ||
| C、-6 | ||
| D、6 |
 某高校招收了100名体育运动员,按身高分组,得到的频率分布表如下左图所示.
某高校招收了100名体育运动员,按身高分组,得到的频率分布表如下左图所示.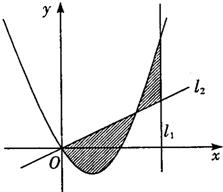 已知二次函数f(x)=3x2-3x,直线l1:x=2和l2:y=3tx(其中t为常数,且0<t<1),直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象所围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).
已知二次函数f(x)=3x2-3x,直线l1:x=2和l2:y=3tx(其中t为常数,且0<t<1),直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象所围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).