题目内容
已知抛物线M:y2=4x与圆N:(x-1)2+y2=r2(其中r为常数,r>0).过点(1,0)的直线l交抛物线M于A,B两点,交圆N于C,D两点,若满足|AC|=|BD|的直线l恰有三条,则r的范围是 .
考点:圆与圆锥曲线的综合
专题:综合题,圆锥曲线的定义、性质与方程
分析:分l⊥x轴与l不与x轴垂直两种情况讨论,当l不与x轴垂直时,设直线l:x=my+1,与抛物线方程y2=4x联立,设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),结合题意,可求得4
=
,继而可得r>2,从而可得答案.
| m2+1 |
| 2r | ||
|
解答:
解:①当l⊥x轴时,过x=1与抛物线交于(1,土2),与圆交于(1,土r),满足题设.
②当l不与x轴垂直时,设直线l:x=my+1,(1)
代入y2=4x,得y2-4my-4=0,
△=16(m2+1),
把(1)代入:(x-1)2+y2=r2得y2=
,
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
∵|AC|=|BD|,
∴y1-y3=y2-y4,y1-y2=y3-y4,
∴4
=
,
即r=2(m2+1)>2,
即r>2时,l仅有三条.
故答案为:(2,+∞).
②当l不与x轴垂直时,设直线l:x=my+1,(1)
代入y2=4x,得y2-4my-4=0,
△=16(m2+1),
把(1)代入:(x-1)2+y2=r2得y2=
| r2 |
| m2+1 |
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
∵|AC|=|BD|,
∴y1-y3=y2-y4,y1-y2=y3-y4,
∴4
| m2+1 |
| 2r | ||
|
即r=2(m2+1)>2,
即r>2时,l仅有三条.
故答案为:(2,+∞).
点评:本题考查直线与圆锥曲线的位置关系,考查等价转化思想与分类讨论思想,求得r=2(m2+1)是关键,考查综合运算能力,属于难题.

练习册系列答案
相关题目
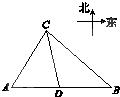 如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站7海里,该轮船从B处沿正西方向航行3海里后到达D处观测站,已知观测站与检查站距离5海里,则此时轮船离港口A有
如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站7海里,该轮船从B处沿正西方向航行3海里后到达D处观测站,已知观测站与检查站距离5海里,则此时轮船离港口A有函数y=x2ex(-2≤x≤2)的最大、最小值分别为( )
A、
| ||
B、4e2,
| ||
| C、4e2,0 | ||
| D、2e2,0 |